强化学习
之前没有深入和系统的学习过强化学习,最近由于科研刚需,上网查资料刚好看到知乎上面有个大佬的强化学习的系列文章,感觉写的很好,于是就把他的文章看了一遍,顺便做了一些笔记,这里记录一下。
原文: https://zhuanlan.zhihu.com/p/111895463
卧槽大佬讲的真的好,笔记记不了一点!!!建议大家都去看原文!
后面可能会自己写一下 MADDPG 和 MATD3 的相关内容,到时候再更新。
2023/10/23 这几天把大佬的强化学习专栏看了一遍了,真的很不错,但是我觉得还是得自己总结一下重难点,且这周五和东大的联合组会轮到我讲了,刚好深入理解一下强化学习算法。所以还是写一下这篇笔记吧!
学习路线: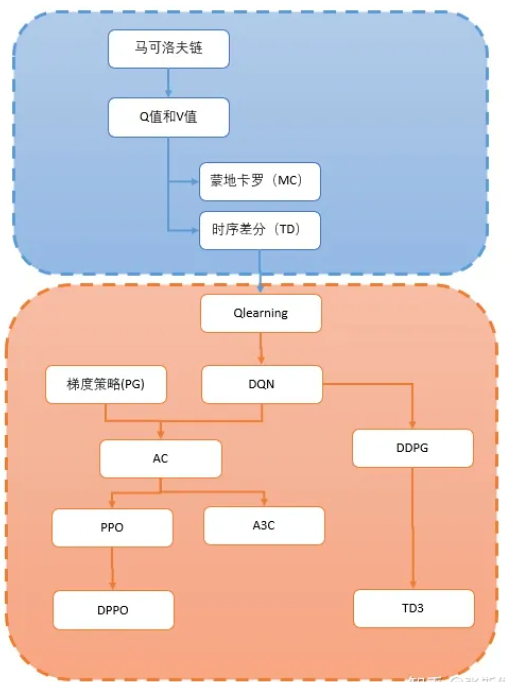
马尔可夫树
强化学习的任务:
- 希望用强化学习的方式,使某个智能体获得独立自主地完成某种任务的能力。
- 智能体学习和工作的地方,称为环境。
- 所谓独立自主,就是智能体一旦启动,就不需要人指挥了。
经典马尔可夫链

- 状态(state):智能体观察到的当前环境的部分或者全部特征。
- 注意:环境的特征可能有许多,但只有智能体能够观察到的特征才算是状态。所以也用observation表示状态。
- 动作(action):智能体做出的具体行为。
- 动作空间就是该智能体能够做出的动作数量。智能体身处十字路口。那么方向就有4个。也就是说,动作空间为4个动作。
- 奖励(reward):智能体在某个状态下采取某个动作所获得的反馈。
- 奖励是一个标量,可以是正数,也可以是负数。奖励越大,说明智能体做的越好。奖励越小,说明智能体做的越差。
RL一般步骤
- 智能体在环境中,观察到状态(S);
- 状态(S)被输入到智能体,智能体经过计算,选择动作(A);
- 动作(A)使智能体进入另外一个状态(S),并返回奖励(R)给智能体。
- 智能体根据返回,调整自己的策略。 重复以上步骤,一步一步创造马尔科夫链。
马尔可夫树
马尔科夫链之所以是现在看到的一条链条。是因为站在现在往过去看,所以是一条确定的路径。但如果往前看,就并不是一条路径,而是充满了各种”不确定性”, 即”马尔可夫树”。
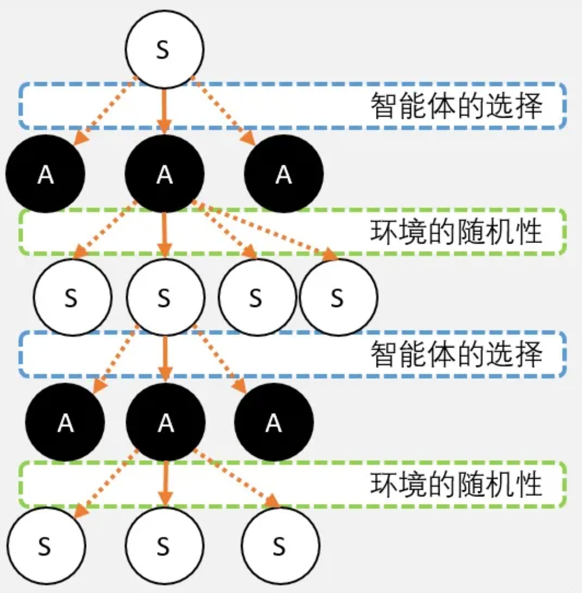
这种”不确定性”来自两个方面:
- 智能体的行动选择(策略)。
- 环境的不确定性。
RL中的Q值和V值
并不能单纯通过R来衡量一个动作的好坏,因为R只是一个瞬时的反馈,而需要的是长期的反馈。在做决策的时候,需要把眼光放远点,把未来的价值换到当前,才能做出选择。
希望可以有一种方法评估我做出每种选择价值。这样,只要看一下标记,以后的事情也不用理,选择那个动作价值更大,就选那个动作就可以了。
- 评估动作的价值称为Q值:它代表了智能体选择这个动作后,一直到最终状态奖励总和的期望。
- 评估状态的价值称为V值:它代表了智能体在这个状态下,一直到最终状态的奖励总和的期望。
价值越高,表示从当前状态到最终状态能获得的平均奖励将会越高。因为智能体的目标数是获取尽可能多的奖励,所以智能体在当前状态,只需要选择价值高的动作就可以了。
V值的定义
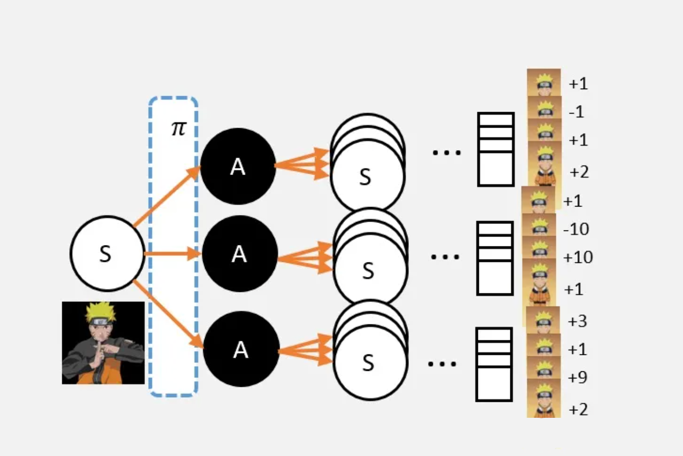
假设现在需要求某状态S的V值,可以这样:
- 从S点出发,并影分身出若干个自己;
- 每个分身按照当前的策略 选择行为;
- 每个分身一直走到最终状态,并计算一路上获得的所有奖励总和;
- 计算每个影分身获得的平均值,这个平均值就是要求的V值。
总结:从某个状态,按照策略 ,走到最终状态很多很多次;最终获得奖励总和的平均值,就是V值。
V值跟选择的策略有很大的关系 。
看这样一个简化的例子,从S出发,只有两种选择,A1,A2;从A1,A2只有一条路径到最终状态,获得总奖励分别为10和20。
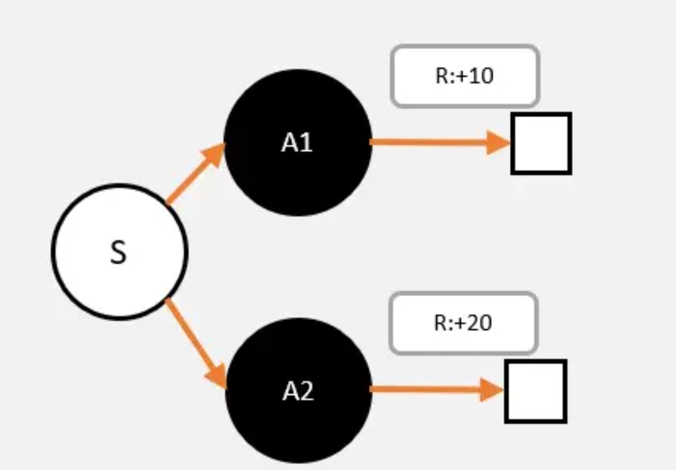


可以看出不同的策略,计算出的V值是不一样的。
Q值的定义
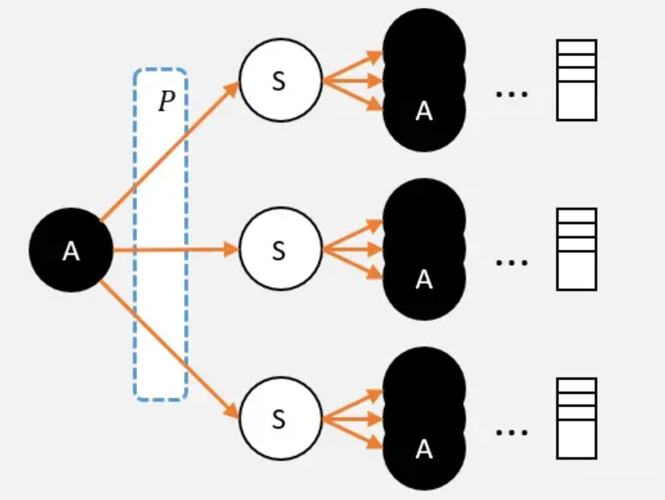
现在需要计算,某个状态S0下的一个动作A的Q值:
- 从A这个节点出发,使用影分身之术;
- 每个影分身走到最终状态,并记录所获得的奖励;
- 求取所有影分身获得奖励的平均值,这个平均值就是要求的Q值。
总结:从某个状态选取动作A,走到最终状态很多很多次;最终获得奖励总和的平均值,就是Q值。
与V值不同,Q值和策略并没有直接相关,而与环境的状态转移概率相关,而环境的状态转移概率是不变的。
V值和Q值关系
Q和V之间是可以相互换算的。
Q值转V值
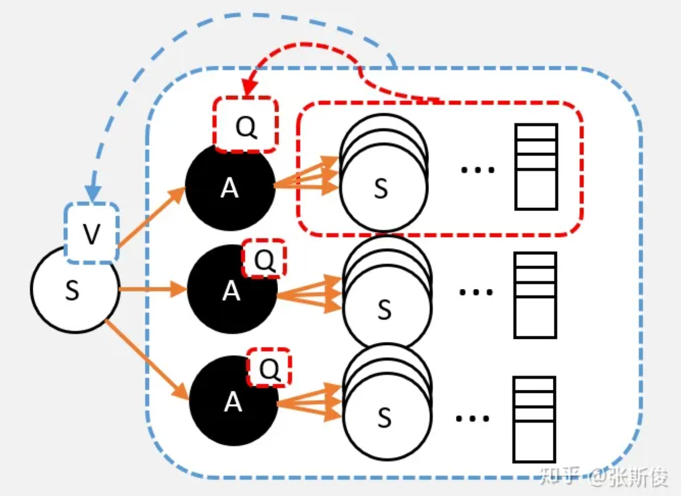
从定义出发,要求的V值,就是从状态S出发,到最终获取的所获得的奖励总和的期望值。也就是蓝色框部分。
S状态下有若干个动作,每个动作的Q值,就是从这个动作之后所获得的奖励总和的期望值。也就是红色框部分。
假设已经计算出每个动作的Q值,那么在计算V值的时候就不需要一直走到最终状态了,只需要走到动作节点,看一下每个动作节点的Q值,根据策略 ,计算Q的期望就是V值了。
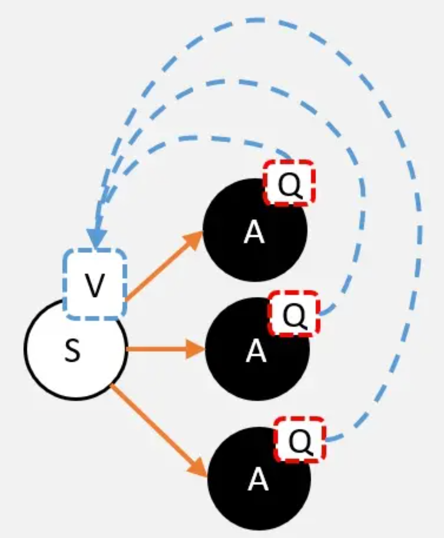
更正式的公式如下: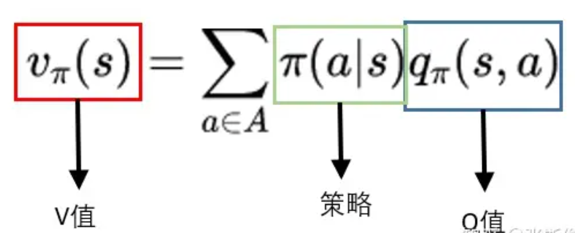
解释:一个状态的V值,就是这个状态下的所有动作的Q值,在策略下的期望。
V值转Q值
Q是V的期望。而这里不需要关注策略,这里是环境的状态转移概率决定的。
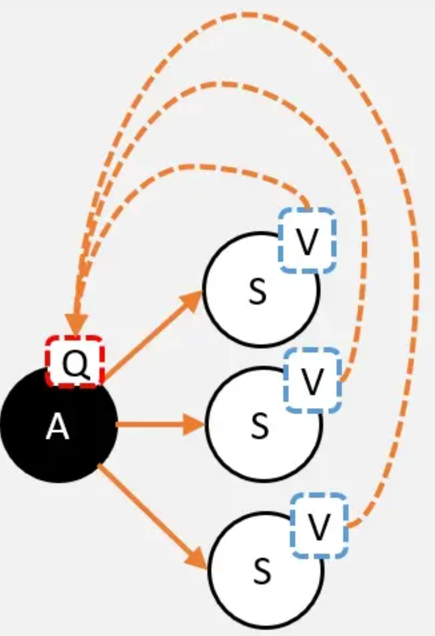
当选择A,并转移到新的状态时,就能获得奖励,必须把这个奖励也算上!
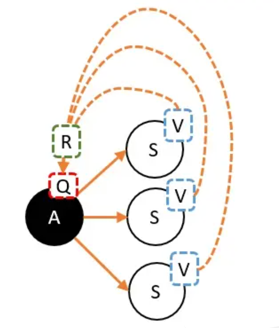
更正式的公式如下: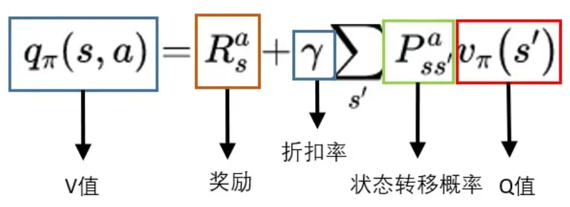
折扣率 在强化学习中,有某些参数是人为主观制定。这些参数并不能推导,但在实际应用中却能解决问题,所以称这些参数为超参数,而折扣率就是一个超参数。
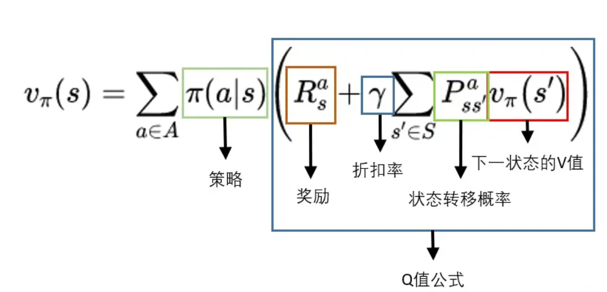
V值转V值
实际应用中,更多会从V到V。其实就是把Q值的公式代入V值的公式。
MC
蒙地卡罗方法(Monte-Carlo)
蒙地卡罗算法
- 把智能体放到环境的任意状态;
- 从这个状态开始按照策略进行选择动作,并进入新的状态。
- 重复步骤2,直到最终状态;
- 从最终状态开始向前回溯:计算每个状态的G值。
- 重复1-4多次,然后平均每个状态的G值,这就是要求的V值。
G值的意义
重要:G值是一个具体的累积奖励值,而Q值和V值是对这个累积奖励值的估计。
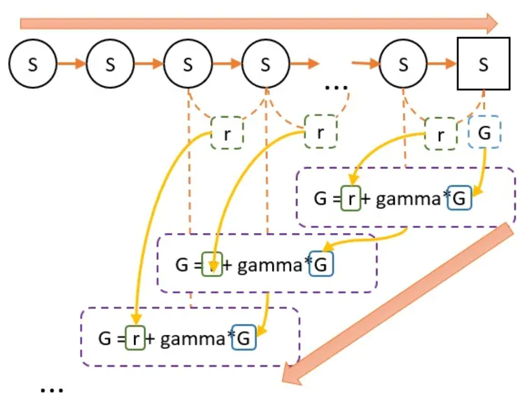
- 第一步,根据策略往前走,一直走到最后,期间什么都不用算,还需要记录每一个状态转移,获得多少奖励r即可。
- 第二步,从终点往前走,一遍走一遍计算G值。G值等于上一个状态的G值(记作G’),乘以一定的折扣(gamma),再加上r。
所以G值的意义在于,在这一次游戏中,某个状态到最终状态的奖励总和(理解时可以忽略折扣值gamma)。
当进行多次试验后,有可能会经过某个状态多次,通过回溯,也会有多个G值。 重复刚才说的,每一个G值,就是每次到最终状态获得的奖励总和。而V值是某个状态下,通过影分身到达最终状态,所有影分身获得的奖励的平均值。
理解:
G的意义:在某个路径上,状态S到最终状态的总收获。V和G的关系:V是G的平均数。
V和策略相关
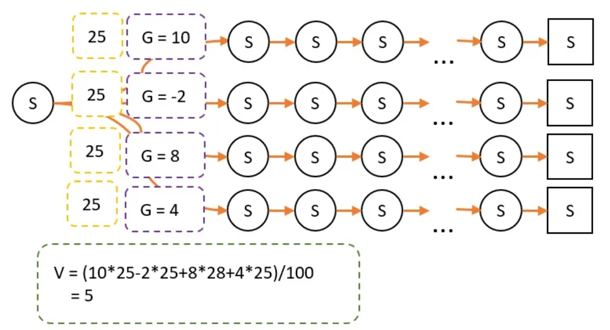
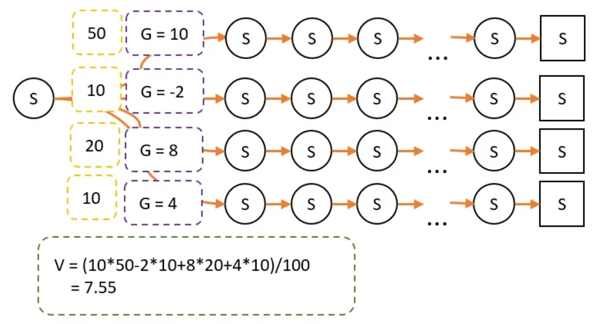
由于策略改变,经过某条路径的概率就会产生变化。因此最终试验经过的次数就不一样了。
蒙地卡罗算法的缺点
每一次游戏,都需要先从头走到尾,再进行回溯更新。如果最终状态很难达到,那可能每一次都要转很久很久才能更新一次G值。
MC的更新公式
上面计算V值其实相当麻烦,因为每一个状态都需要建立一个空间,记录每个轨迹下的G值。
那有没有一种方法,可以用更少的空间计算V值呢?当然有,那就是增量更新。
增量更新
现在只需要记录之前的平均值V,新加进来的G,和次数N。把V和G的差,除以N,然后再加到原来的平均值V上,就能计算到新的V值。
V_new = (V_old - G) * (1 / N) + V_old
- V_old:原来的V值
- G:这一次回溯后,计算出来的G值
- N: 这个状态被经过多少次
- V_new:新计算出来的V值
更进一步
这样计算还是比较麻烦,甚至可以不用记录N,把(1/N)设置成为一个固定的数,例如0.1、0.2(还记得超参数吗?)。把这个值称为学习率。
这就相当于,新来的G和V_old的差的十分之一,会被加到V_new上!也就是说,每一次G都会引导V增加一些或者减少一些,而这个V值慢慢就会接近真正的V值。
这里的G,也称为V的更新目标。
而学习率就可以理解为,每次V向目标靠近的幅度;学习率越大,表示向G靠近的幅度越大,反之则越小。
两种理解方式

TD
时序差分算法TD(Temporal-Difference)
TD和MC的比较
TD算法对蒙地卡罗(MC)进行了改进:
- 和蒙地卡罗(MC)不同:
TD算法只需要走N步,不用走到终点,就可以开始回溯更新。 - 和蒙地卡罗(MC)一样:需要先走N步,每经过一个状态,把奖励r记录下来。然后开始回溯。
- 那么,状态的V值怎么算呢?其实和蒙地卡罗一样,就假设N步之后,就到达了最终状态了。
- 假设“最终状态”上之前没有走过,所以这个状态上的纸是空白的。这个时候就当这个状态为0.
- 假设“最终状态”上已经走过了,这个状态的V值,就是当前值。然后开始回溯。
直观理解
从A状态,经过1步,到B状态。什么都不管就当B状态是最终状态了。此时N = 0,也叫做TD(0)。
但B状态本身就带有一定的价值,也就是V值。其意义就是从B状态到最终状态的总价值期望。
.png)
假设B状态的V值是对的,那么,通过回溯计算,就能知道A状态的更新目标了。
更新公式
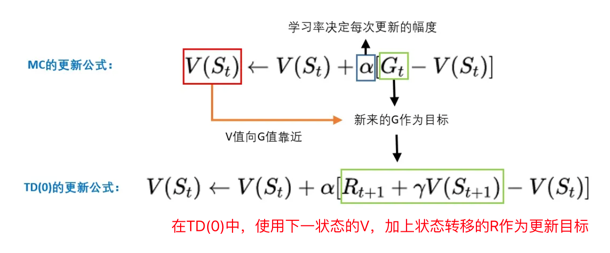
TD并走走完整段路程,而是半路就截断。用半路的路牌,更新当前的路牌。 所以只需要把MC的更新目标,改为TD的更新目标即可。
在MC,G是更新目标,而在TD,只不过把更新目标从G,改成r+gamma*V
Q-learning
之前用TD(0)预估状态价值V:%E6%9B%B4%E6%96%B0%E5%85%AC%E5%BC%8F.png)
图解:%E5%9B%BE%E8%A7%A3.png)
TD能够用在V值,那么也能用在计算Q值上。
TD之于Q值估算
现在用上TD的思路。 在St,智能体根据策略pi,选择动作At,进入S(t+1)状态,并获得奖励R。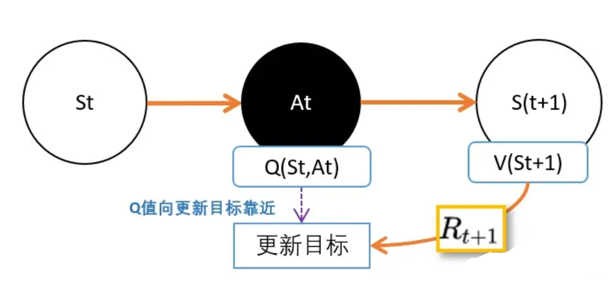
- V(St+1)的意义是,在St+1到最终状态获得的奖励期望值。
- Q(St,At)的意义是,在Q(St,At)到最终状态获得的奖励期望值。
在这里要估算两个东西,一个是V值,一个是Q值。人们想到用下一个动作的Q值代替V值。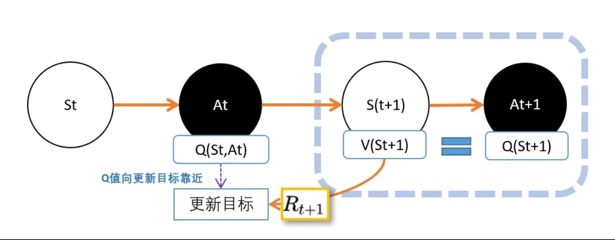
但是,这里就有个坑:虽然从状态St+1到动作At+1之间没有奖励反馈,但还是不能直接用At+1的Q价值,代替St+1的V价值。
因为马尔可夫树!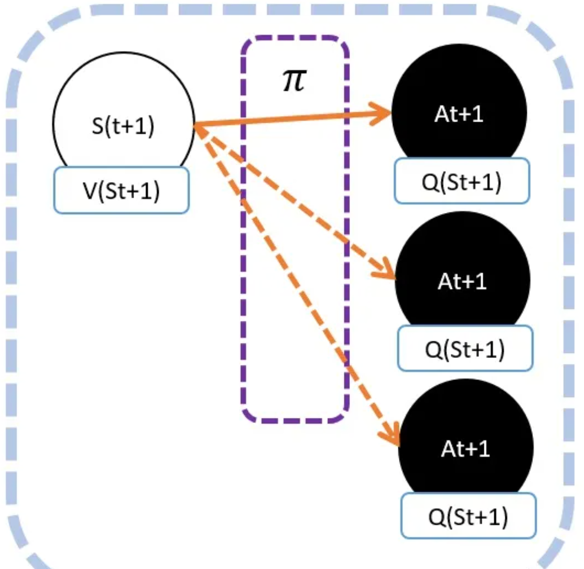
在St+1下,可能有很多动作At+1。不同动作的Q值自然是不同的。 所以Q(St+1,At+1)并不能等价于V(St+1)。
虽然不相等,但不代表不能用其中一个来代表V(St+1)。人们认为有个可能的动作产生的Q值能够一定程度代表V(St+1)。
- 在相同策略下产生的动作At+1。这就是
SARSA。 - 选择能够产生最大Q值的动作At+1。这就是
Qlearning。
SARSA
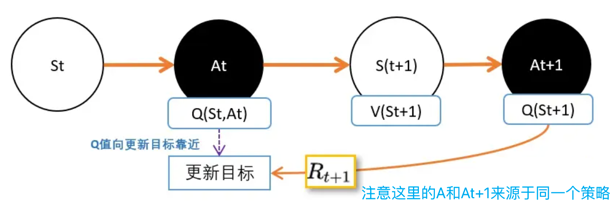
其实SARSA和上一篇说的TD估算V值几乎一模一样,只不过挪了一下,从V改成Q了。
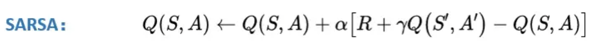
%E4%B8%8ESARSA%E5%AF%B9%E6%AF%94.png)
注意: 这里的At+1是在同一策略产生的。也就是说,St选At的策略和St+1选At+1是同一个策略。这也是SARSA和Qlearning的唯一区别。
Qlearning
Qlearning将能够产生最大Q值的动作At+1的Q值作为V(St+1)的替代。
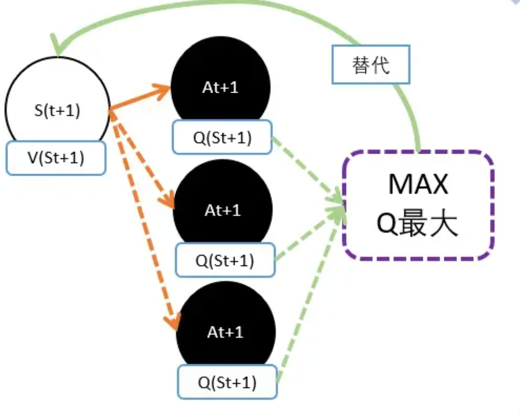
理解:因为需要寻着的是能获得最多奖励的动作,Q值就代表能够获得今后奖励的期望值。所以选择Q值最大的,也只有最大Q值能够代表V值。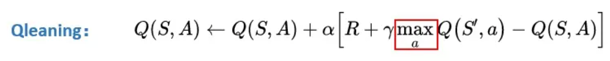
Q(S,a)的更新目标:在Qlearning,用下一状态St+1的最大Q值替代St+1的V值。V(St+1)加上状态转移产生的奖励R。
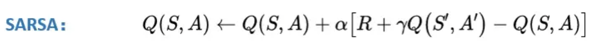
Qleanring和SARSA,两者的差别仅仅在Qlearning中多了个max。
总结
- Qlearning和SARSA都是基于TD(0)的。不过在之前的介绍中,用TD(0)估算状态的V值。而Qlearning和SARSA估算的是动作的Q值。
- Qlearning和SARSA的核心原理,是用下一个状态St+1的V值,估算Q值。
- 既要估算Q值,又要估算V值会显得比较麻烦。所以用下一状态下的某一个动作的Q值,来代表St+1的V值。
- Qlearning和SARSA唯一的不同,就是用什么动作的Q值替代St+1的V值。
- SARSA 选择的是在St同一个策略产生的动作。
- Qlearning 选择的是能够产生最大的Q值的动作。
Qlearning 实现
TODO: 这里所有算法的代码仅仅是看了一遍,还没有自己手写一遍,等这周联合组会后再说。
深度神经网络
深度强化学习:用深度神经网络辅助强化学习。
原理
假如知道X,y有关系,那么不妨先设这个关系可以通过函数Magic(X)获得。也就是说Magic(X)=y。
这在手写数字识别中,X就是需要识别的图片,y就是识别出来的数字分类。 任务就是需要求这个Magic函数。.png)
现在假设有另外一个函数Magic’(),这个函数是由深度神经网络构成。
在刚开始的时候,很明显Magic’(X) 并不等于y,例如输入手写图片8,Magic’()计算后,认为数字8只有20%,但数字9有40%。
…但这没所谓,因为这是刚开始。任务是让Magic’(X)产生的结果y’ 和 y尽量接近。
y’和真实y之间的差距,叫损失,也就是loss。有时候也会把y称为目标(target),因为任务就是让Magic’(X)越来越靠近这个目标。
衡量loss的方法有很多,定义不同loss对神经网络学习有着重大差别,话题太大暂时不展开。
loss越大,表示和目标差距越远;loss越小,表示和目标越近,当小到一定值,那么就可以认为Magic’(X)和Magic(X)函数非常接近,可以通过Magic’(X)计算出y。
当有许许多多这样的y,经过许许多多轮后。Magic’就越来越贴近Magic。也就是说X和y之间的关系就能越来越好地表达出来。
.png)
放大镜下的深度神经网络
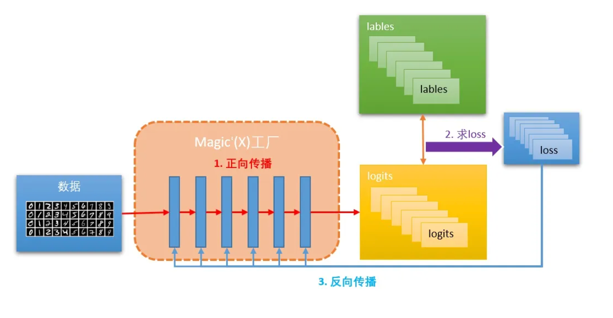
现在可以把深度神经网络的Magic函数,看成是一个数据加工厂。而X就是要进行加工的数据。
为了让这个数据加工厂运行得更快,通常需要把要加工的数据X变得更标准一些。
例如图片的尺寸大小,有多少通道的颜色等等,然后分批(batch),输入工厂。
在输入工厂的时候,会有一个‘大门’,称为输入层,去检查数据是否已经按照工厂的标准整理好。
数据工厂里有很多车间,按照流水线排列。和一般的自动化车间一样,需要定义好这个车间的操作标准。
一般称这些车间叫层。这些层都已经封装好在tensorflow、tensorlayer、pytorch等里面了。常用的层包括:Dense、Conv2D、LSTM、Reshape、Flatten等。
最终,数据工厂会把原数据X,加工成产品y'(也叫做:logits)。从源数据加工成产品的过程,叫正向传播。
但产品y’是否是一个合格的产品,还需要真正的y(lables)作为标准去鉴定。把鉴定出来的差距就是loss。
工厂根据鉴定结果,以梯度下降的方式,反向传递给每个车间,告诉车间要如何调整各自的参数,让源数据和产出y’能够对应起来。
经过N个批次(batch)的数据输入,然后鉴别,工厂调整。最后工厂就能达到生产标准了。也就是说magic函数已经被训练好了。
DQN
DQN: TD + 神经网络
在Qlearning中,有一个Qtable,记录着在每一个状态下,各个动作的Q值。
Qtable的作用是当输入状态S,通过查表返回能够获得最大Q值的动作A。也就是需要找一个S-A的对应关系。
这种方式很适合格子游戏。因为格子游戏中的每一个格子就是一个状态,但在现实生活中,很多状态并不是离散而是连续的。
用神经网络解决Qlearning中动作离散的问题,让动作变成连续的,这就是DQN。
Deep network + Qlearning = DQN
神经网络万能函数(神经网络)Magic(X)接受输入一个状态S,它能告诉我,每个动作的Q值是怎样的。
理解DQN中的神经网络
Qtable三维可视化: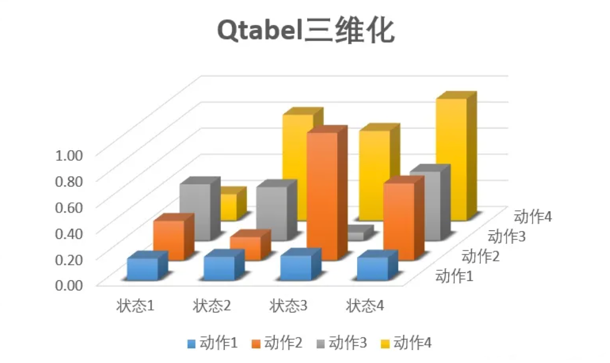
图中每根柱子的高度,表示状态S下,选择动作A的Q值。
现在用函数来表示,相当于要扭曲一条曲线,这条曲线穿过了离散状态下的所有点。
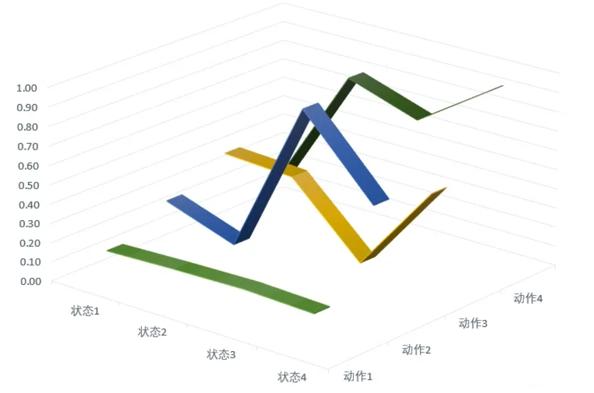
从二维状态看: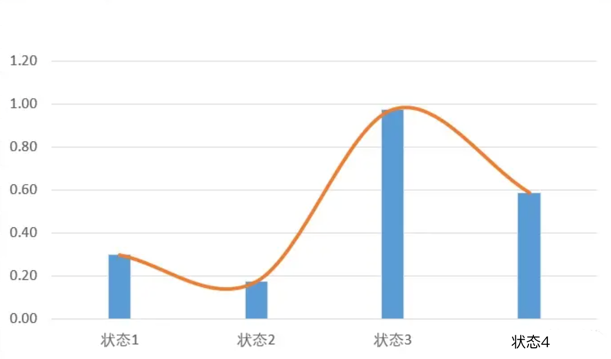
所以现在不但可以取状态3和状态4,还可以取状态3.5的Q值。
现在就很清楚了,其实Qlearning和DQN并没有根本的区别。只是DQN用神经网络,也就是一个函数替代了原来Qtable而已。
更新目标
更新目标就是Magic(X),最终要向这个Magix(X)靠近。
在Qlearning,用下一状态St+1的最大Q值替代St+1的V值。V(St+1)加上状态转移产生的奖励R。就是Q(S,a)的更新目标。
DQN和Qlearning一样: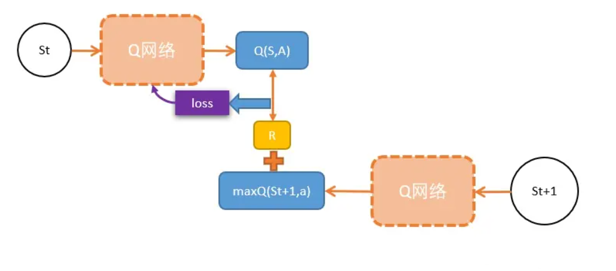
假设需要更新当前状态St下的某动作A的Q值:Q(S,A),可以这样做:
- 执行A,往前一步,到达St+1;
- 把St+1输入Q网络,计算St+1下所有动作的Q值;
- 获得最大的Q值加上奖励R作为更新目标;
- 计算损失
- Q(S,A)相当于有监督学习中的logits
- maxQ(St+1) + R 相当于有监督学习中的lables
- 用mse函数,得出两者的loss
- Loss = (Q(S, A) - [gamma * maxQ(St+1) + R])^2
- 用loss更新Q网络。(反向传播)
通常会使用一个折扣因子 gamma 来考虑未来奖励的重要性。折扣因子 gamma 的作用是对未来奖励进行衰减,使得当前时刻的奖励比未来时刻的奖励更具有影响力。
也就是,用Q网络估算出来的两个相邻状态的Q值,他们之间的距离,就是一个r的距离。这个就是更新目标Target = R + gamma * maxQ(St+1)
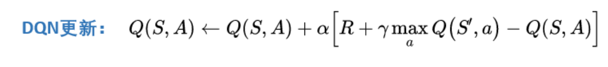
总结:
- 其实DQN就是Qlearning扔掉Qtable,换上深度神经网络。
- 解决连续型问题,如果表格不能表示,就用函数,而最好的函数就是深度神经网络。
- 和有监督学习不同,深度强化学习中,需要自己找更新目标。通常在马尔科夫链体系下,两个相邻状态状态差一个奖励r经常能够作为更新目标。
DQN 实现
TODO: 这里所有算法的代码仅仅是看了一遍,还没有自己手写一遍,等这周联合组会后再说。
Double DQN
经验回放
经验回放解决了强化学习中的两个问题: 训练网络数据采集慢 和 过度拟合
当然这个慢是对比网络训练的速度。在强化学习中,网络训练经过GPU的加速,比起游戏来时快很多的。所以训练的瓶颈一般在智能体跟环境互动的过程中。 如果能把互动过程中的数据,都存起来,当数据最够多的时候,再训练网络,那么就快很多了。
把每一步的s,选择的a,进入新的状态s’,获得的奖励r,新状态是否为终止状态。都存在一个叫回放缓存的地方(replay buffer)。
当智能体与环境互动期间,就会不断产生这样一条一条数据。 数据1: 数据2: 数据3: ….
当数据量足够,达到设定一个batch的大小,便从中抽出一个batch大小的数据,把这笔数据一起放入网络进行训练。
训练之后继续进行游戏,继续把新产生的数据添加到回放缓存里…
就这样每次都随机抽出一个batch大小的数据训练智能体。这样,以前产生的数据同样也能用来训练数据了, 效率自然更高。
使用经验回放除了使训练更高效,同时也减少了训练产生的过度拟合的问题。
过度拟合,放到人身上就是过度依赖局部经验了。
就像孩子发现爸爸有胡子,就认为所有男人都有胡子一样。
同样,在有监督学习中,如果只给模型看少量的几张图,并且告诉模型这是猫。这样模型就只会从这几张图学习到猫的特点,而更多的猫模型可能就不认得了。说这就是过度拟合造成的,导致模型不够健壮。
DQN的问题
DQN的目标:Target = R + gamma * maxQ(St+1)
目标本身就包含一个Q网络,理论上是没有问题的,但,这样会造成Q网络的学习效率比较低,而且不稳定。
如果把训练神经网络比喻成射击游戏,在target中有Q网络的话,就相当于在射击一个移动靶,因为每次射击一次,靶就会挪动一次。相比起固定的靶,无疑加上了训练的难度。
要解决这个问题,就把移动靶弄成是固定的靶,先停止10秒。10后挪动靶再打新的靶。这就是Fixed Q-targets的思路。
Fixed Q-targets
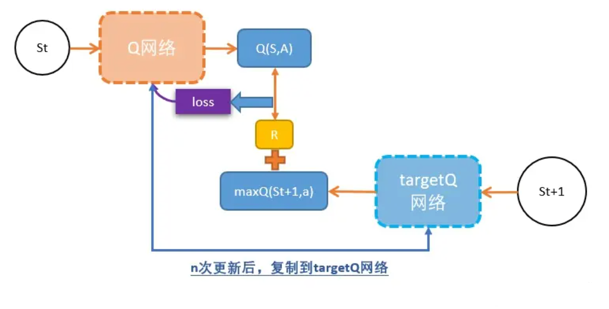
其他地方和DQN一样,唯一不同是用了两个Q网络。
- 原来的Q网络,用于估算Q(s);
- targetQ网络, targetQ自己并不会更新,也就是它在更新的过程中是固定的,用于计算更新目标。
y = r + gamma * max(targetQ(s'))- 进行N次更新后,就把新Q网络的参数赋值给旧Q网络,保持训练的稳定性。
Double DQN
DQN有一个显著的问题,就是DQN估计的Q值往往会偏大。这是由于Q值是以下一个s’的Q值的最大值来估算的,但下一个state的Q值也是一个估算值,也依赖它的下一个state的Q值…,这就导致了Q值往往会有偏大的的情况出现。
这个思路也很直观。如果只有一个Q网络,Q值的估计往往偏大。那就用两个Q网络,因为两个Q网络的参数有差别,所以对于同一个动作的评估也会有少许不同。选取评估出来较小的值来计算更新目标。这样就能有效避免Q网络估值偏大的情况发生了。
另外一种做法也需要用到两个Q网络:Q1网络推荐能够获得最大Q值的动作;Q2网络计算这个动作在Q2网络中的Q值。
Double DQN 实现
TODO: 这里所有算法的代码仅仅是看了一遍,还没有自己手写一遍,等这周联合组会后再说。
Duel DQN
Dueling DQN原理
回到Qtable, 原来会直接预估Q值表的数据,现在改为需要预估两个值:S值和A值。即Q = S + A
- S: 在特定状态下采取任何行动的平均价值,也就是该state下的Q值的平均数。
- A: 在特定状态下采取特定动作相对于采取平均动作的优势。A的平均值为0。
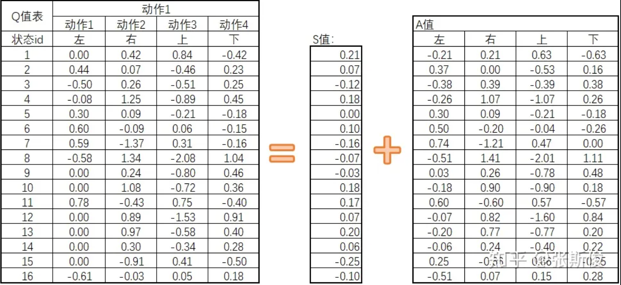
普通DQN的Q网络,可以理解用一个曲线去拟合Qtable的Q值。现在取一个截面,表示当取某个S下,各个动作的Q值。
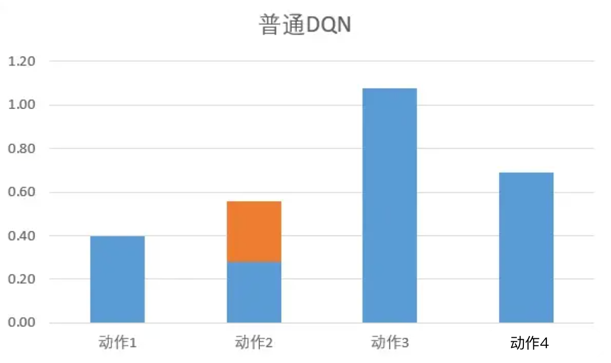
普通DQN在提升某个状态下的S值时,只会提升某个动作。
Dueling DQN: 在网络更新的时候,由于有A值之和必须为0的限制,所以网络会优先更新S值。S值是Q值的平均数,平均数的调整相当于一次性S下的所有Q值都更新一遍。
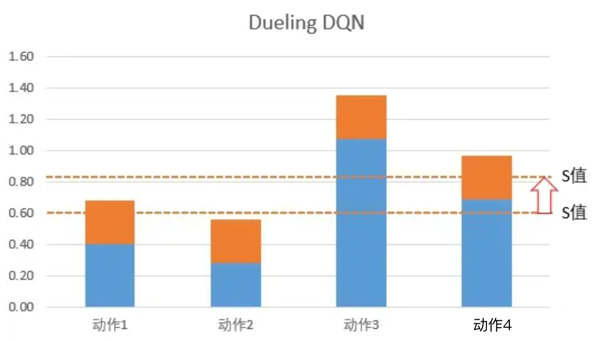
如上图,橙色虚线是平均值,也就是S值。 所以网络在更新的时候,不但更新某个动作的Q值,而是把这个状态下,所有动作的Q值都调整一次。这样,就可以在更少的次数让更多的值进行更新。
这样调整最后的数值是对的吗?放心,在DuelingDQN,只是优先调整S值。但最终的target目标是没有变的,所以最后更新出来也是对的。
网络架构
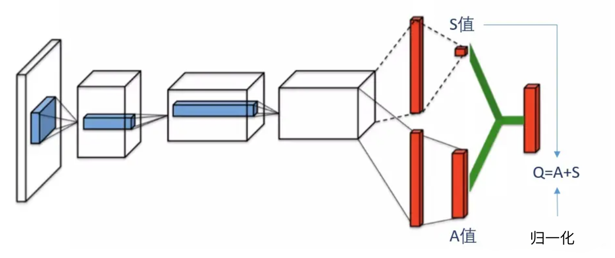
可以把dueling DQN分为三部分:
- 第一部分:和普通DQN一样,用来处理和学习数据。
- 第二部分:计算svalue,就是让网络预估的平均值。
- 第三部分:计算avalue,和svalue一样,都是从h2层输入到该层。然后对avalue进行归一化处理,也就是增加“A值的平均值为0”的限制。
- 归一化的处理很简单,求A值的平均值,然后用A值减去平均值即可。A-mean(A)
DeulingDQN的实现很简单,只需要修改Q网络的网络架构就可以了。而且可以和其他DQN的技巧,例如经验回放,固定网络,双网络计算目标等可以共用。
Duel DQN 实现
TODO: 这里所有算法的代码仅仅是看了一遍,还没有自己手写一遍,等这周联合组会后再说。
PG
策略梯度(Policy Gradient)
之前的MC、TD、Qlearning、DQN都是基于值的方法,就是一定要算Q值和V值。但事实上最终目的是要找一个策略,能获得最多的奖励。
这就是策略梯度(Policy Gradient)
PG原理
认识到:
DQN: TD + 神经网络PG: MC + 神经网络
PG中的Magic(state):
当输入state的时候,输出pi,告诉智能体这个状态,应该如何应对: = magic(state)。如果智能体的动作是对的,那么就让这个动作获得更多被选择的几率;相反,如果这个动作是错的,那么这个动作被选择的几率将会减少。
复习一下蒙地卡罗:
从某个state出发,然后一直走,直到最终状态。然后从最终状态原路返回,对每个状态评估G值。 所以G值能够表示在策略下,智能体选择的这条路径的好坏。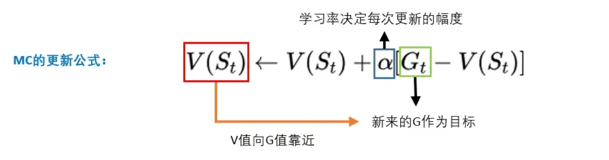
直观感受PG
从某个state出发,可以采取三个动作。 假设当前智能体对这一无所知,那么,可能采取平均策略 Pi0 = [33%,33%,33%]。智能体出发,选择动作A,到达最终状态后开始回溯,计算得到 G = 1。
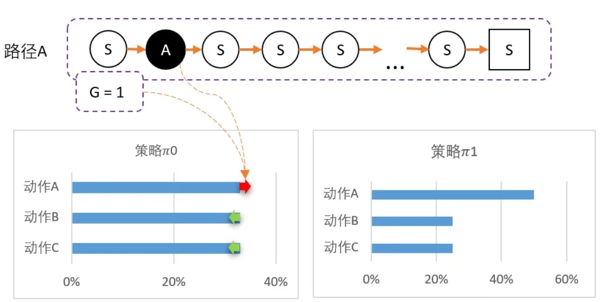
更新策略,因为该路径选择了A而产生的,并获得G = 1;因此要更新策略:让A的概率提升,相对地,BC的概率就会降低。 计算得新策略为: Pi1 = [50%,25%,25%]。虽然B概率比较低,但仍然有可能被选中。第二轮刚好选中B。智能体选择了B,到达最终状态后回溯,计算得到 G = -1。
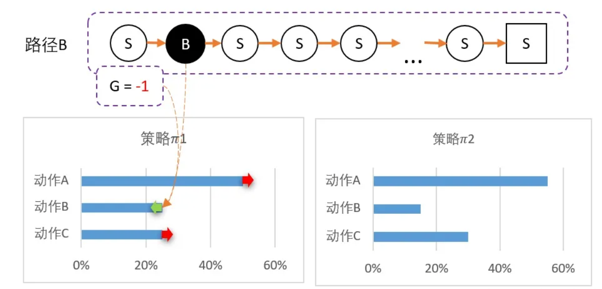
此时对B动作的评价比较低,并且希望以后会少点选择B,因此要降低B选择的概率,而相对地,AC的选择将会提高。计算得新策略为: Pi2 = [55%,15%,30%]。最后随机到C,回溯计算后,计算得G = 5。
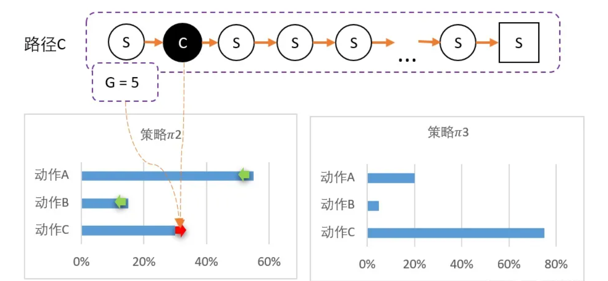
C比A还要多得多。因此这一次更新,C的概率需要大幅提升,相对地,AB概率降低。 Pi3 = [20%,5%,75%]。
PG 实现
TODO: 这里所有算法的代码仅仅是看了一遍,还没有自己手写一遍,等这周联合组会后再说。
AC
AC: PG + DQN(TD + 神经网络)
PG利用带权重的梯度下降方法更新策略,而获得权重的方法是MC计算G值。MC需要完成整个游戏过程,直到最终状态,才能通过回溯计算G值。这使得PG方法的效率被限制。
改为TD可以解决上面的问题。接下来又面临另一个问题:
在PG,需要计算G值;那么在TD中,应该怎样估算每一步的Q值呢?答案是用神经网络。
也就是说,Actor-Critic,其实是用了两个网络:
两网络都输入状态S,Critic比Actor多一个St+1:
- 一个网络输出策略,负责选择动作,把这个网络成为Actor;
- 一个网络负责计算每个动作的分数,把这个网络成为Critic。
TD-error
在DQN预估的是Q值,在AC中的Critic,估算的是V值。不估算Q值是因为效果不好。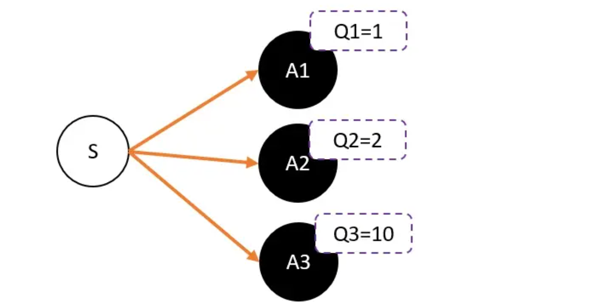
假设用Critic网络,预估到S状态下三个动作A1,A2,A3的Q值分别为1,2,10。 但在开始的时候,采用平均策略,于是随机到A1。于是用策略梯度的带权重方法更新策略,这里的权重就是Q值。于是策略会更倾向于选择A1,意味着更大概率选择A1。结果A1的概率就持续升高…
这就掉进了正数陷阱。明明希望A3能够获得更多的机会,最后却是A1获得最多的机会。这是为什么呢?
因为Q值用于是一个正数,如果权重是一个正数,那么相当于提高对应动作的选择的概率。权重越大,调整的幅度将会越大。其实当有足够的迭代次数,这个是不用担心这个问题的。因为总会有机会抽中到权重更大的动作,因为权重比较大,抽中一次就能提高很高的概率。
但在强化学习中,往往没有足够的时间去和环境互动。这就会出现由于运气不好,使得一个很好的动作没有被采样到的情况发生。要解决这个问题,可以通过减去一个baseline,令到权重有正有负。而通常这个baseline,选取的是权重的平均值。减去平均值之后,值就变成有正有负了。而Q值的期望(均值)就是V。
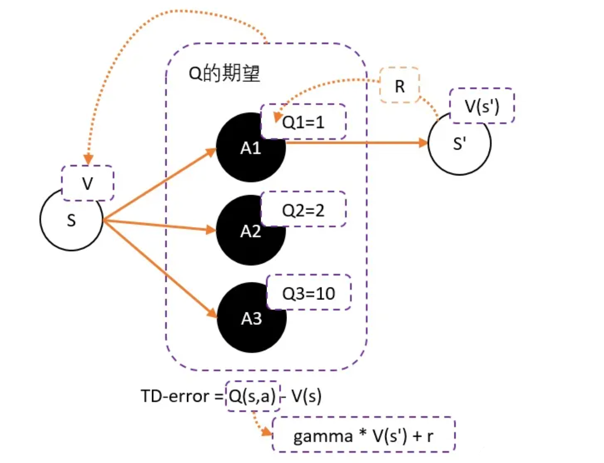
可以得到更新的权重:Q(s,a)-V(s),Q(s,a)用gamma * V(s') + r 代替。
得到TD-error:TD-error = gamma * V(s') + r - V(s)
和之前DQN的更新公式非常像,只不过DQN的更新用了Q,而TD-error用的是V。如果Critic是用来预估V值,而不是原来讨论的Q值。那么,这个TD-error是用来更新Critic的loss了!没错,Critic的任务就是让TD-error尽量小。然后TD-error给Actor做更新。
至于为啥TD-error是用来更新Critic的loss呢?
取TD-error的方差来作为critic的loss,其实类似于DQN中的Q网络,认为下个状态的估算值比目前状态的Q值更精确,所以把下个状态的估算值作为目标,来更新Q网络。此处单看critic网络吗,其目的仅在于预测V值,所以它的估算值也要向更准确的下个阶段估算值来靠近,即TD-error越来越小。
再来看actor网络,TD-error在其中的作用仅是更新网络时的权重,其与动作的选择并无直接关系。前期TD-error较大,每次更新时,动作的概率都会进行相对较大的改动,随着不断地训练,动作的概率逐渐成熟,TD-error越来越小,所以每次更新时对动作概率的改动也随之减小。
总结
- 为了避免正数陷阱,希望Actor的更新权重有正有负。因此,把Q值减去他们的均值V。有:
Q(s,a)-V(s) - 为了避免需要预估V值和Q值,把Q和V统一;由于
Q(s,a) = gamma * V(s') + r - V(s)。所以得到TD-error公式:TD-error = gamma * V(s') + r - V(s) TD-error就是Actor更新策略时候,带权重更新中的权重值;- 现在Critic不再需要预估Q,而是预估V。而根据马可洛夫链所学,知道TD-error就是Critic网络需要的loss,也就是说,Critic函数需要最小化TD-error。
算法
- 定义两个network:Actor 和 Critic
- 进行N次更新。
- 从状态s开始,执行动作a,得到奖励r,进入状态s’
- 记录的数据。
- 把输入到Critic,根据公式: TD-error = gamma * V(s’) + r - V(s) 求 TD-error,并缩小TD-error
- 把输入到Actor,计算策略分布。
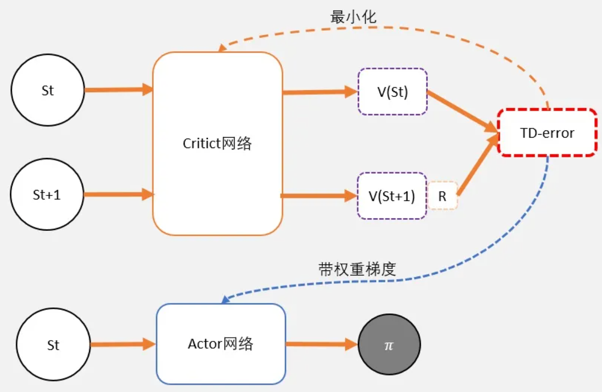
可以看出:在PG,智能体需要从头一直跑到尾,直到最终状态才开始进行学习。 在AC,智能体采用是每步更新的方式。
AC 实现
TODO: 这里所有算法的代码仅仅是看了一遍,还没有自己手写一遍,等这周联合组会后再说。
PPO
PPO是基于AC框架的
正态分布
首先要想办法处理连续动作的输出问题。
- 离散动作:离散动作就像一个个的按钮,按一个按钮就能智能体就做一个动作。
- 连续动作:相当于按钮不但有开关的概念,而且还有力度大小的概念。就像开车,不但是前进后退转弯,并且要控制油门踩多深,刹车踩多少的,转弯时候转向转多少的问题。
在离散动作空间的问题中,最终输出的策略呈现出下面形式: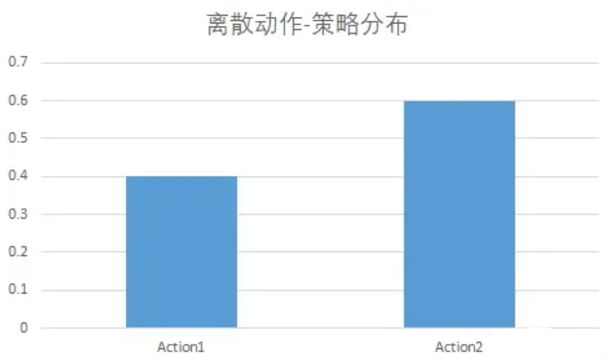
假设动作空间有只有action1 和 action2,有40%的概率选择action1 ,60%概率选择action2。即在此状态下的策略分布: pi = [0.4, 0.6]。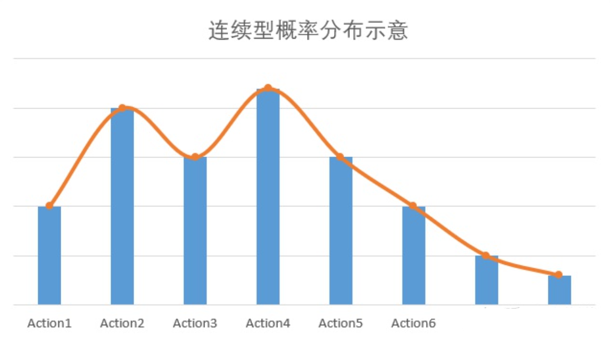
在连续型,不再用数组表示,而是用函数表示。例如,策略分布函数 : P = (action)代表在策略下,选择某个action的概率P。
用神经网络预测输出的策略是一个固定的shape,而不是连续的。那又什么办法可以表示连续型的概率呢?可以假定策略分布函数服从一个概率分布,例如正态分布。
这样,只用两个参数就可以表示了。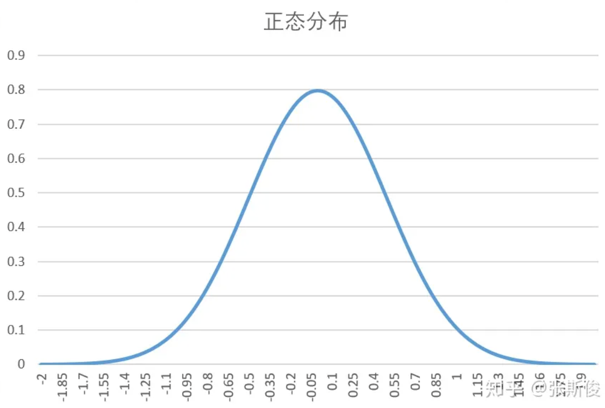
正态分布:
- sigma:表示方差,当sigma越大,图像越扁平;sigma约小,图像越突出。而最大值所在的位置,就是中轴线。
- mu:表示平均数,也就是整个正态分布的中轴线。mu的变化,表示整个图像向左右移动。
神经网络直接输出mu和sigma,就能获得整个策略的概率密度函数了。现在,当要按概率选择一个动作时,就只需要按照这个概率密度函数,随机抽取一个数,就能得到一个动作了。
AC的问题
上面的正态分布解决了AC处理连续状态空间的问题。但是,AC还有一个问题:AC产生的数据,只能进行1次更新,更新完就只能丢掉,等待下一次的数据。
行为策略:行为策略是代理在与环境交互时采取行动的策略。它决定了代理在当前状态下选择每一个可能的行动的概率分布。不是当前策略,用于产出数据。
目标策略:目标策略是代理在训练过程中试图优化的策略。它是代理最终想要学习到的最优策略,它通常被设计为最大化期望累积奖励。会更新的策略,是需要被优化的策略。
在线策略:在线策略是指在与环境交互时实时地采取行动,并根据实时的反馈来更新策略。也就是说,代理在与环境互动时,采取行动并根据实际结果来调整策略。目标策略和行为策略是同一个策略,那么是在线策略。
- 实时更新:在线策略会根据每次与环境交互的结果来进行即时更新。
- 依赖实时反馈:在线策略依赖于实时的环境反馈来进行学习和调整。
离线策略:离线策略是指在事先收集好的数据集上进行训练,而不需要实时地与环境交互。也就是说,代理使用事先收集的经验数据来训练策略,而不依赖于实时环境反馈。目标策略和行为策略不是同一个策略,那么是离线策略。
- 离线数据:训练过程中不需要实时地与环境进行交互,可以使用先前收集的数据。
- 无需环境互动:训练过程中不需要实时环境反馈。
例子:
如果在智能体和环境进行互动时产生的数据打上一个标记。标记这是第几版本的策略产生的数据,例如 1, 2… 10。现在智能体用的策略 10,需要更新到 11。如果算法只能用 10版本的产生的数据来更新,那么这个就是在线策略;如果算法允许用其他版本的数据来更新,那么就是离线策略。
例如PG,就是一个在线策略。因为PG用于产生数据的策略(行为策略),和需要更新的策略(目标策略)是一致。 而DQN则是一个离线策略。会让智能体在环境互动一定次数,获得数据。用这些数据优化策略后,继续跑新的数据。但老版本的数据仍然是可以用的。也就是说,产生数据的策略,和要更新的目标策略不是同一个策略。所以DQN是一个离线策略。
为什么PG和AC中的Actor更新策略,不能像DQN一样把数据存起来,只能用一次产生的数据?
看一个例子: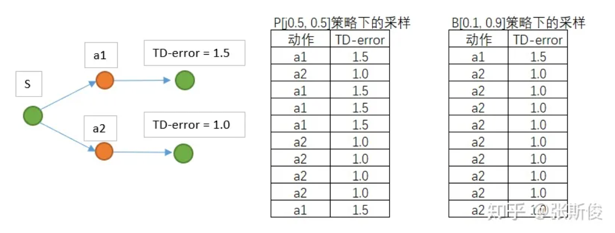
TD-error 可以理解为从状态S 到下一个状态动作的价值,所以动作1的 TD-error 大,所以希望选择动作1的概率大
假设,已知在同一个环境下,有两个动作可以选择。现在两个策略,分别是P和B: P: [0.5,0.5] B: [0.1,0.9]
现在按照两个策略,进行采样;也就是分别按照这两个策略,以S状态下出发,与环境进行10次互动。获得如图数据。那么,可以用B策略下获得的数据,更新P吗?
答案是不行,回顾PG算法,PG算法会按照TD-error作为权重,更新策略。权重越大,更新幅度越大;权重越小,更新幅度越小。
但可以从如下示意图看到,如果用行动策略B[0.1,0.9]产出的数据,对目标策略P进行更新,动作1会被更新1次,而动作2会更新9次。虽然动作1的TD-error比较大,但由于动作2更新的次数更多,最终动作2的概率会比动作1的要大。

这不是期望看到的更新结果,因为动作1的TD-error比动作2要大,希望的是选择概率动作1的能更多。由此可以明白,在策略更新的时候不能使用其他策略产生的数据。
为什么DQN可以多次重复使用数据?
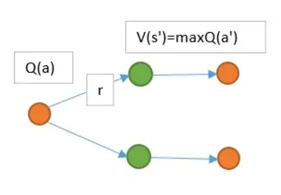
两个角度:
- 更新Q值,和策略无关。 在同一个动作出发,可能会通往不同的state,但其中的概率是状态转移概率决定的,与环境有关,而不是策略所决定的。所以产生的数据和策略并没有关系。
- 在DQN的更新中是有”目标”的。 虽然目标比较飘忽,但每次更新,其实都是尽量向目标靠近。无论更新多少次,最终都会在目标附近徘徊。但PG算法,更新是不断远离原来的策略分布的,所以远离多少、远离的次数比例都必须把握好。
在Actor-Critic (AC) 方法中,Critic 网络更新的是状态值函数(Value Function)V,而不是动作值函数(Q函数)。
重要性采样技术
在PPO中,如果想使用策略B的数据来更新策略P,那就要把TD-error乘上一个重要性权重(importance weight)。
在这里IW = P(a)/ B(a)
就是 IW = 目标策略出现动作a的概率 / 行为策略出现a的概率。
- 目标策略:要更新的策略。
- 行为策略:数据的策略。
这里是用策略B的数据来更新策略P,所以P是目标策略,B是行为策略。
现在即使用P策略: [0.5,0.5]进行更新,a1提升的概率也会比a2的更多。
PPO使用重要性采样技术把AC从在线策略变成离线策略。
N步更新
之前的TD叫做TD(0),而N步更新为TD(n)。可以看成TD(0)其实是TD(n)的一种特殊情况。
.png)
如图,实际上只需要计算最后的V(s’),根据这个估算的V(s’), 反推经过的所有state的V值。这个其实和PG估算G的过程是一样的,只不过并不需要走到最后,而是中途截断,用网络估算。
V = R + gamma * V(s')
总结
实际上,P策略和B策略差异并不能太大,为了能处理这个问题,有两个做法,PPO1 和 PPO2 。主流是PPO2。
- 用AC来解决连续型控制问题。方法是输入mu和sigma,构造一个正态分布来表示策略;
- PPO延展了TD(0),变成TD(N)的N步更新;
- AC是一个在线算法,但为了增加AC的效率,希望把它变成一个离线策略,这样就可以多次使用数据了。为了解决这个问题,PPO使用了重要性采样。
PPO 实现
TODO: 这里所有算法的代码仅仅是看了一遍,还没有自己手写一遍,等这周联合组会后再说。
DDPG
DDPG,全称是deep deterministic policy gradient,深度确定性策略梯度算法。
- deep: 深度网络。
- policy gradient: PG
- deterministic: 其实DDPG也是解决连续控制型问题的的一个算法,不过和PPO不一样,PPO输出的是一个策略,也就是一个概率分布,而DDPG输出的直接是一个动作。
DDPG更接近DQN,是用一个actor去弥补DQN不能处理连续控制性问题的缺点。
回顾DQN
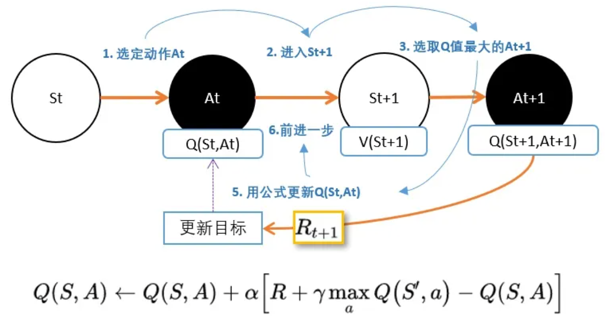
从公式中也能看出,DQN不能用于连续控制问题原因,是因为maxQ(s’,a’)函数只能处理离散型的。这个就是DDPG中的Actor的功能: 用一个magic函数,直接替代maxQ(s’,a’)的功能。也就是说,期待输入状态s,magic函数返回动作action的取值,这个取值能够让q值最大。
理解DDPG
DDPG中Critic的功能,像是DQN的深度网络,用一张布去覆盖Qlearning中的Qtable。
当把某个state输入到DDPG的Actor中的时候,相当于在这块布上做沿着state所在的位置剪开,会看到这个边缘是一条曲线。
注意: 这条曲线很像概率分布,但要一定注意,这里并不是策略,也不是PPO和AC中的V值。是在某个状态state下,选择某个动作值的时候,能获得的Q值。
Actor的任务就是在寻找这个曲线的最高点,然后返回能获得这个最高点,也是最大Q值的动作。 所以,DDPG其实并不是PG,并没有做带权重的梯度更新。而是在梯度上升,在寻找最大值。 这也就解释了,为什么DDPG是一个离线策略,但可以多次更新却不用importance sampling。这是因为这个算法就是DQN,和策略没有直接的关系。
DDPG
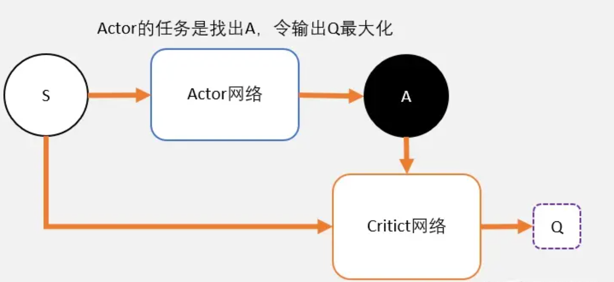
整理下:
Critic
- Critic网络的作用是预估Q,虽然它还叫Critic,但和AC中的Critic不一样,这里预估的是Q不是V;
- 注意Critic的输入有两个:动作和状态,需要一起输入到Critic中;
- Critic网络的loss其还是和AC一样,用的是TD-error。
Actor
- 和AC不同,Actor输出的是一个动作;
- Actor的功能是,输出一个动作A,这个动作A输入到Critic后,能够获得最大的Q值。
- Actor的更新方式和AC不同,不是用带权重梯度更新,而是用梯度上升。
和DQN一样,DDPG更新的时候如果更新目标在不断变动,会造成更新困难。所以DDPG和DQN一样,用了固定网络(fix network)技术,就是先冻结住用来求target的网络。在更新之后,再把参数赋值到target网络。
所以实际做的时候使用了4个网络:actor, critic, Actor_target, cirtic_target。
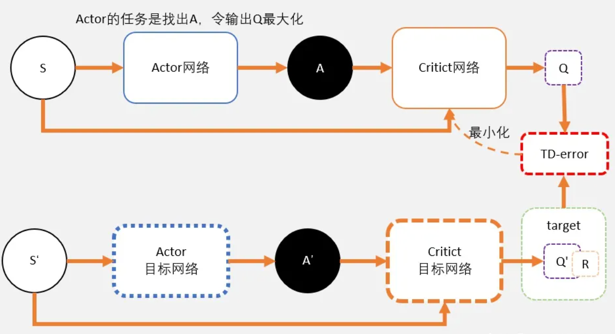
目标网络只是用在求target的过程中。如果不是求target用的,就不用目标网络。
DDPG 实现
TODO: 这里所有算法的代码仅仅是看了一遍,还没有自己手写一遍,等这周联合组会后再说。
TD3
Twin Delayed Deep Deterministic policy gradient algorithm,双延迟深度确定性策略梯度
TD3是对DDPG的优化,三个重要优化。
double network
DDPG起源于DQN,DQN有一个众所周知的问题就是Q值会被过高估计。这是因为用argmaxQ(s’)去代替V(s’),去评估Q(s)。当每一步都这样做的时候,很容易就会出现高估Q值的情况。
在TD3中,用了两套网络估算Q值,相对较小的那个作为更新的目标。这就是TD3的基本思路。
回顾DDPG:
通过Critic网络估算动作的A值。一个Critic的评估可能会较高。所以加一个。
TD3需要用到6个网络: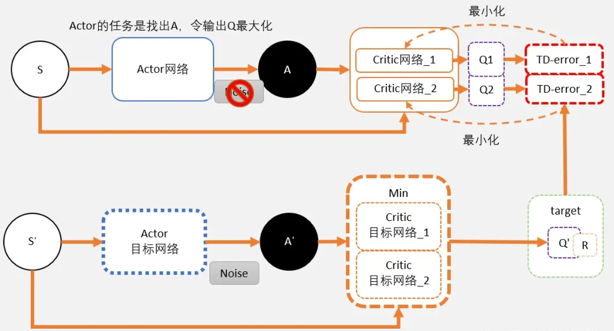
在目标网络中,估算出来的Q值会用min()函数求出较小值。以这个值作为更新的目标。这个目标会更新两个网络 Critic网络_1 和 Critic网络_2。 这两个网络是完全独立,他们只是都用同一个目标进行更新。 剩余的就和DDPG一样了。过一段时间,把学习好的网络赋值给目标网络。
Critic部分的学习
只有在计算Critic的更新目标时,才用target network。其中就包括了一个Policy network,用于计算A’;两个critic target Q network ,用于计算两个Q值:Q1(A’) 和Q2(A’)。
Q1(A’) 和Q2(A’) 取最小值 min(Q1,Q2) 将代替DDPG的 Q(a’) 计算更新目标,也就是说: target = min(Q1,Q2) * gamma + r
target 将会是 Q_network_1 和 Q_network_2 两个网络的更新目标。
TD-error_1 = gamma * min(Q1,Q2) + r - Q1TD-error_2 = gamma * min(Q1,Q2) + r - Q2
既然更新目标是一样的,那么为什么还需要两个网络呢?
虽然更新目标一样,两个网络会越来越趋近与和实际q值相同。但由于网络参数的初始值不一样,会导致计算出来的值有所不同。所以可以有空间选择较小的值去估算q值,避免q值被高估。
Actor部分的学习
DDPG网络图像上就可以想象成一张布,覆盖在qtable上。当输入某个状态的时候,相当于这块布上的一个截面,能够看到在这个状态下的一条曲线。
而actor的任务,就是用梯度上升的方法,寻着这条线的最高点。
对于actor来说,其实并不在乎Q值是否会被高估,他的任务只是不断做梯度上升,寻找这条最大的Q值。随着更新的进行Q1和Q2两个网络,将会变得越来越像。所以用Q1还是Q2,还是两者都用,对于actor的问题不大。
actor延迟更新
actor更新的delay,也就是说相对于critic可以更新多次后,actor再进行更新。
为什么要这样做呢?
回到qnet拟合出来的那块”布”上。 qnet在学习过程中,的q值是不断变化的,也就是说这块布是不断变形的。所以要寻着最高点的任务有时候就挺难为的actor了。

可以想象,本来是最高点的,当actor好不容易去到最高点;q值更新了,这并不是最高点。这时候actor只能转头再继续寻找新的最高点。更坏的情况可能是actor被困在次高点,没有找到正确的最高点。
所以可以把Critic的更新频率,调的比Actor要高一点。让critic更加确定,actor再行动。
target网络噪声
TD3中,价值函数的更新目标每次都在action上加一个小扰动,这个操作就是target policy smoothing regularization
为什么要这样呢?
回到关于“布”的想象。 在DDPG中,计算target的时候,输入时s_和a_,获得q,也就是这块布上的一点A。通过估算target估算另外一点s,a,也就是布上的另外一点B的Q值。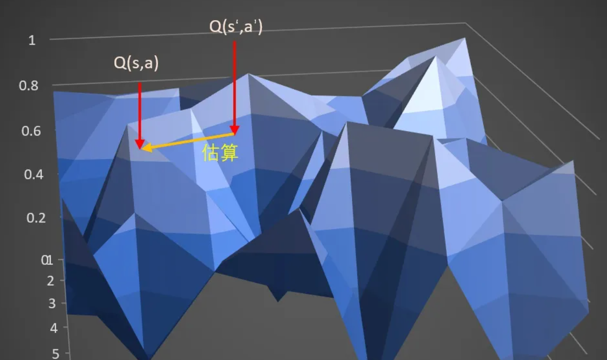
在TD3中,计算target时候,输入s_到actor输出a后,给a加上噪音,让a在一定范围内随机。这又什么好处呢。
好处就是,当更新多次的时候,就相当于用A点附近的一小部分范围(准确来说是在s_这条线上的一定范围)的去估算B,这样可以让B点的估计更准确,更健壮。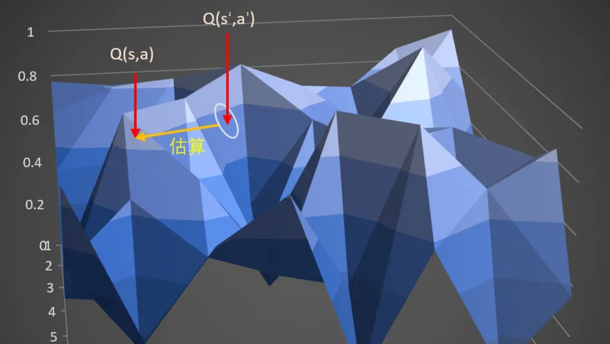
这里注意三个地方:
- 在实验中,同样加上了了noise。这个时候的noise是为了更充分地开发整个游戏空间。
- 计算target的时候,actor加上noise,是为了预估更准确,网络更有健壮性。
- 更新actor的时候,不需要加上noise,这里是希望actor能够寻着最大值。加上noise并没有任何意义。
TD3 实现
TODO: 这里所有算法的代码仅仅是看了一遍,还没有自己手写一遍,等这周联合组会后再说。
这里的TD3仅针对自己的实验平台实现了类似于MATD3的效果,但是实际上,没有明确的MATD3。后面再考虑在gym上实现以加深理解。
A3C
强化学习的一个难点,智能体的用于学习的数据,需要智能体和环境不断进行交互。和一般有监督学习的先比,数据数量太少了。
在算法没有更大进步的时候,有人就想出,如果有多个智能体和环境进行互动,那么每个智能体都能产出数据,这些数据就可以一起给模型进行学习了。
由此诞生了A3C。
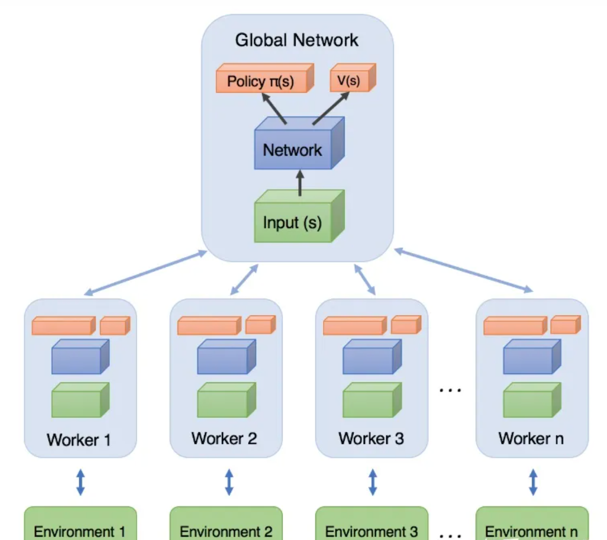
注意几点:
- 在A3C中,worker不仅要和环境互动,产生数据,而且要自己从这些数据里面学习到“心得”。这里的所谓新的,其实就是计算出来的梯度;需要强调的是,worker向全局网络汇总的是梯度,而不是自己探索出来的数据。
在这一点上,很容易和DPPO混淆。DPPO和A3C,也是一个分布式的架构,但work自己并不学习,而是提交数据让全局网络学习。
- worker向全局网络汇总梯度之后,并应用在全局网络的参数后,全局网络会把当前学习到的最新版本的参数,直接给worker。worker按照最新的网络继续跟环境做互动。互动后,再把梯度提交,获取新的参数…… 如此循环。
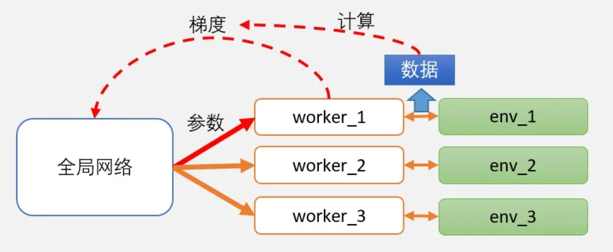
A3C 实现
TODO: 这里所有算法的代码仅仅是看了一遍,还没有自己手写一遍,等这周联合组会后再说。
DPPO
DPPO和A3C的思路其实是一致的,希望用多个智能体同时和环境互动,并对全局的PPO网络进行更新。
在A3C,需要跑数据并且计算好梯度,再更新全局网络。这是因为AC是一个在线的算法,所以在更新的时候,产生数据的策略和更新的策略需要时同一个网络。所以不能把worker产出的数据,直接给全局网络计算梯度用。
但PPO解决了离线更新策略的问题,所以DPPO的工人只需要提供数据给全局网络,由全局网络从数据中直接学习。
DPPO 实现
TODO: 这里所有算法的代码仅仅是看了一遍,还没有自己手写一遍,等这周联合组会后再说。
写在最后
到这里,传统强化学习的总结就结束了,后面由于我的科研方向是多智能体强化学习,会更新关于多智能体强化学习的算法。









