MARL
由于我的科研方向是
多智能体强化学习,且由于研一忙于课程和一些开源项目,导致我对一些科研方面的算法理解不够充分。刚好,最近一次和东大的联合组会轮到我讲了,借此深度理解一下这些算法。
在这篇笔记中,我会总结我的直系学长推荐我先看的多智能体强化学习知乎专栏内容,然后如果有时间,再总结我导师之前发给我让我看的论文。相关链接我会放在下面。
知乎专栏:https://www.zhihu.com/column/c_1061939147282915328
基础知识与博弈
引言
在多智能体系统中,每个智能体通过与环境进行交互获取奖励值(reward)来学习改善自己的策略,从而获得该环境下最优策略的过程就多智能体强化学习。
在单智能体强化学习中,智能体所在的环境是稳定不变的,但是在多智能体强化学习中,环境是复杂的、动态的,因此给学习过程带来很大的困难。
- 维度爆炸:在单体强化学习中,需要存储状态值函数或动作-状态值函数。在多体强化学习中,状态空间变大,联结动作空间随智能体数量指数增长,维度非常大,计算复杂。
- 目标奖励确定困难:多智能体系统中每个智能体的任务可能不同,但是彼此之间又相互耦合影响。奖励设计的优劣直接影响学习到的策略的好坏。
- 不稳定性:在多智能体系统中,多个智能体是同时学习的。当同伴的策略改变时,每个智能体自身的最优策略也可能会变化,这将对算法的收敛性带来影响。
- 探索-利用:探索不光要考虑自身对环境的探索,也要对同伴的策略变化进行探索,可能打破同伴策略的平衡状态。每个智能体的探索都可能对同伴智能体的策略产生影响,这将使算法很难稳定,学习速度慢。
多智能体系统中智能体之间可能涉及到合作与竞争等关系,引入博弈的概念,将博弈论与强化学习相结合可以很好的处理这些问题。
纳什均衡

完全混合策略
若一个策略对于智能体动作集中的所有动作的概率都大于0,则这个策略为一个完全混合策略。
纯策略
若智能体的策略对一个动作的概率分布为1,对其余的动作的概率分布为0,则这个策略为一个纯策略。
零和博弈
零和博弈中,两个智能体是完全竞争对抗关系,则 R1 = - R2 。在零和博弈中只有一个纳什均衡值,即使可能有很多纳什均衡策略,但是期望的奖励是相同的。
一般和博弈
一般和博弈是指任何类型的矩阵博弈,包括完全对抗博弈、完全合作博弈以及二者的混合博弈。在一般和博弈中可能存在多个纳什均衡点。
矩阵博弈和线性规划求双智能体矩阵博弈的纳什均衡策略可以看这篇:https://zhuanlan.zhihu.com/p/53474965
Minimax-Q
论文:Markov games as a framework for multi-agent reinforcement learning
Minimax-Q算法应用于两个玩家的零和随机博弈中。Minimax-Q中的Minimax指的是使用minimax方法构建线性规划来求解每个特定状态s的阶段博弈的纳什均衡策略。Q指的是借用Q-learning中的TD方法来迭代学习状态值函数或动作-状态值函数。
在两玩家零和随机博弈中,给定一个状态s,则定义第i个智能体的状态值函数如下:意义为,每个智能体最大化在与对手博弈中最差情况下的期望奖励值。

理想情况,如果算法能够对每一个状态-动作对访问无限次,那么该算法能够收敛到纳什均衡策略。但是在上述算法中存在几个缺点:
- 在第5步中需要不断求解一个线性规划,这将造成学习速度的降低,增加计算时间。
- 为了求解第5步,智能体i需要知道所有智能体的动作空间,这个在分布式系统中将无法满足。
- 只满足收敛性,不满足合理性。Minimax-Q算法能够找到多智能体强化学习的纳什均衡策略,但是假设对手使用的不是纳什均衡策略,而是一个较差的策略,则当前智能体并不能根据对手的策略学习到一个更优的策略。该算法无法让智能体根据对手的策略来调节优化自己的策略,而只能找到随机博弈的纳什均衡策略。这是由于Minimax-Q算法是一个对手独立算法(opponent-independent algorithm),不论对手策略是怎么样的,都收敛到该博弈的纳什均衡策略。就算对手采用一个非常弱的策略,当前智能体也不能学习到一个比纳什均衡策略更好的策略。
Nash Q-Learning
论文:Nash Q-learning for general-sum stochastic games
Nash Q-Learning算法是将Minimax-Q算法从零和博弈扩展到多人一般和博弈的算法。在Minimax-Q算法中需要通过Minimax线性规划求解阶段博弈的纳什均衡点,拓展到Nash Q-Learning算法就是使用二次规划求解纳什均衡点。Nash Q-Learning算法在合作性均衡或对抗性均衡的环境中能够收敛到纳什均衡点,其收敛性条件是,在每一个状态s的阶段博弈中,都能够找到一个全局最优点或者鞍点,只有满足这个条件,Nash Q-Learning算法才能够收敛。与Minimax-Q算法相同,Nash Q-Learning算法求解二次规划的过程也非常耗时,降低了算法的学习速度。
其算法流程如下:

该算法需要观测其他所有智能体的动作ai与奖励值ri。并且与Minimax-Q算法一样,只满足收敛性,不满足合理性。只能收敛到纳什均衡策略,不能根据其他智能体的策略来优化调剂自身的策略。
Friend-or-Foe Q-Learning
论文:Friend-or-foe Q-learning in general-sum games
Friend-or-Foe Q-Learning(FFQ)算法也是从Minimax-Q算法拓展而来。为了能够处理一般和博弈,FFQ算法对一个智能体i,将其他所有智能体分为两组,一组为i的friend帮助i一起最大化其奖励回报,另一组为i的foe对抗i并降低i的奖励回报,因此对每个智能体而言都有两组。这样一个n智能体的一般和博弈就转化为了一个两智能体的零和博弈。
其纳什均衡策略求解方法如下所示:
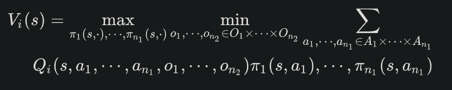
算法流程如下:

有一种利用Minimax-Q算法进行多人博弈方法为,两队零和博弈,将所有智能体分成两个小组进行零和博弈。两队零和博弈中每一组有一个leader才控制这一队智能体的所有策略,获取的奖励值也是这一个小组的整体奖励值。
FFQ算法没有team learder,每个人选择自己动作学习自己的策略获得自己的奖励值,但是为了更新值,每个智能体需要在每一步观测其他所有friend与foe的执行动作。
FFQ与Minimax-Q算法一样都需要利用线性规划,因此算法整体学习速度会变慢。
WoLF Policy Hill-Climbing
论文:Multiagent learning using a variable learning rate

WolF是指,当智能体做的比期望值好的时候小心缓慢的调整参数,当智能体做的比期望值差的时候,加快步伐调整参数。
PHC是一种单智能体在稳定环境下的一种学习算法。该算法的核心就是通常强化学习的思想,增大能够得到最大累积期望的动作的选取概率。该算法具有合理性,能够收敛到最优策略。
其算法流程如下:

为了将PHC应用于动态环境中,将WoLF与PHC算法结合,使得智能体获得的奖励在比预期差时,能够快速调整适应其他智能体策略变化,当比预期好时谨慎学习,给其他智能体适应策略变化的时间。并且WoLF-PHC算法能够收敛到纳什均衡策略,并且具备合理性,当其他智能体采用某个固定策略使,其也能收敛到一个目前状况下的最优策略而不是收敛到一个可能效果不好的纳什均衡策略处。在WoLF-PHC算法中,使用一个可变的学习速率 δ 来实现WoLF效果,当策略效果较差时使用 δl ,策略效果较好时使用 δw ,并且满足 δl > δw 。还有一个优势是,WoLF-PHC算法不用观测其他智能体的策略、动作及奖励值,需要更少的空间去记录Q值,并且WoLF-PHC算法是通过PHC算法进行学习改进策略的,所以不需要使用线性规划或者二次规划求解纳什均衡,算法速度得到了提高。虽然WoLF-PHC算法在实际应用中取得了非常好的效果,并且能够收敛到最优策略。但是其收敛性在理论上一直没有得到证明。
其算法流程如下所示:

关于MiniMax-Q、Nash Q-Learning、Friend-or-Foe Q-Learning、WoLF Policy Hill-Climbing算法的详细介绍可以看这篇:https://www.cnblogs.com/zuti666/p/16909220.html 和 https://zhuanlan.zhihu.com/p/53563792
MADDPG
论文:Multi-Agent Actor-Critic for Mixed Cooperative-Competitive Environments
OpenAI 2017发表在NIPS 上的一篇文章。主要是将AC算法进行了一系列改进,使其能够适用于传统RL算法无法处理的复杂多智能体场景。
传统RL算法面临的一个主要问题是由于每个智能体都是在不断学习改进其策略,因此从每一个智能体的角度看,环境是一个动态不稳定的,这不符合传统RL收敛条件。并且在一定程度上,无法通过仅仅改变智能体自身的策略来适应动态不稳定的环境。由于环境的不稳定,将无法直接使用之前的经验回放等DQN的关键技巧。policy gradient算法会由于智能体数量的变多使得本就有的方差大的问题加剧。
MADDPG算法具有以下三点特征:
- 通过学习得到的最优策略,在应用时只利用局部信息就能给出最优动作。
- 不需要知道环境的动力学模型以及特殊的通信需求。
- 该算法不仅能用于合作环境,也能用于竞争环境。
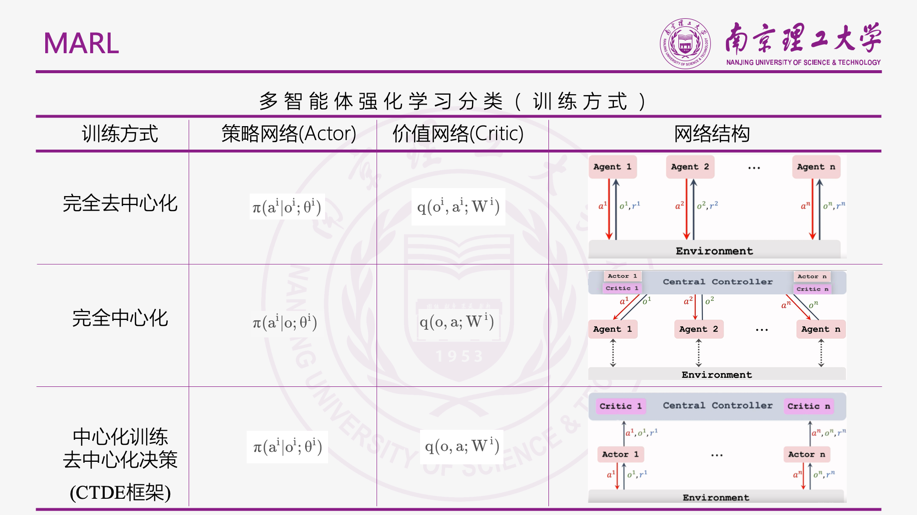
MADDPG算法具有以下三点技巧:
- 集中式训练,分布式执行:训练时采用集中式学习训练critic与actor,使用时actor只用知道局部信息就能运行。critic需要其他智能体的策略信息,本文给了一种估计其他智能体策略的方法,能够只用知道其他智能体的观测与动作。
- 改进了经验回放记录的数据。为了能够适用于动态环境,每一条信息由(x, x’, a1,…, an, r1,…, rn)组成,X = (o1,…, on)。表示每个智能体的观测。
- 利用策略集合效果优化(policy ensemble):对每个智能体学习多个策略,改进时利用所有策略的整体效果进行优化。以提高算法的稳定性以及鲁棒性。
背景知识
DQN
深度Q网络(deep Q-network)
SPG
随机策略梯度(stochastic policy gradient)

DPG
确定性策略梯度(deterministic policy gradient)

MADDPG
多智能体AC设计
MADDPG集中式的学习,分布式的应用。因此允许使用一些额外的信息(全局信息)进行学习,只要在应用的时候使用局部信息进行决策就行。这点就是Q-learning的一个不足之处,Q-learning在学习与应用时必须采用相同的信息。所以这里MADDPG对传统的AC算法进行了一个改进,Critic扩展为可以利用其他智能体的策略进行学习,这点的进一步改进就是每个智能体对其他智能体的策略进行一个函数逼近。

估计其他智能体策略

策略集合优化

相关PPT



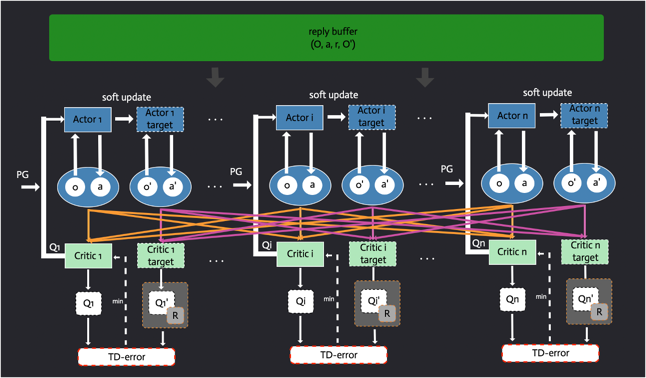
IQL
论文:Multiagent Cooperation and Competition with Deep Reinforcement Learning
Independent Q-Learning
本文讲的是介绍如何将DQN用到Multi-agent问题中,并表示最直接的方法就是,智能体把其他智能体喝环境看作整体,每个智能体之间的决策相互独立(用原文的话说就是each agent is controlled by an independent Deep Q-Network)。
IQL发现,两个智能体都独立采用DQN,在不修改除了reward外的任何参数、细节,agent都能取得不错的成绩。这说明IQL可以作为多智能体强化学习的baseline。
IQL(independent Q-learning)算法非常简单暴力地给每个智能体执行一个Deep-Q-learning算法。IQL把单智能体Deep-Q-learning算法直接应用在多智能体学习领域,各个智能体是各自为政的。这是此类算法的一个极端。
其他没啥要讲的。。。
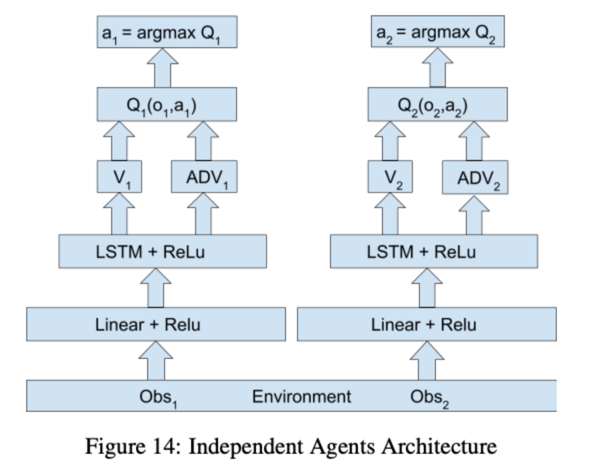
COMA
论文:Counterfactual Multi-Agent Policy Gradients
COMA (counterfactual multi-agent) 使用一个集中式的critic网络计算优势函数A,统一给Agenti计算对应的actioni分别去执行。所谓CTDE(central training decentralize execution)。COMA是把Actor-critic单智能体算法直接应用在多智能体学习领域,各个智能体按照集中的critic网络指令行事,它们是完全协作关系。这是此类算法的另一个极端。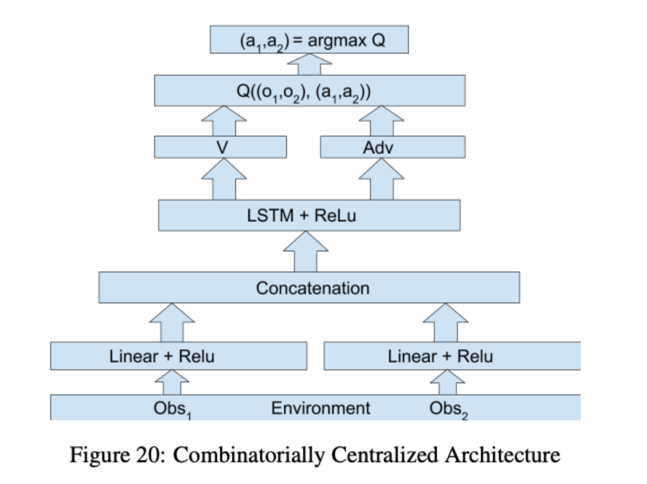
多智能体强化学习算法必然都是在IQL和COMA两个算法之间做平衡。Agent既不能完全独立行事,也不能完全按中心节点指令行事。
那么这些算法都在解决什么问题呢?
只要模型共享Qtot值函数,团队奖励值ri有可能仅仅是某几个智能体获得的,其它智能体并没有做贡献但缺获得了奖励值ri。这就是所谓多智能体信用分配(credit assignment)问题。
在COMA算法中,为了解决多智能体信用分配问题,提出了优势函数A(遍历Agenti动作空间μi里的所有动作,而保持其它Agent的动作空间μ–不变,计算每个Agenti的参数值),用来计算反事实基线(counterfactual baseline)。

这个思想来自difference reward。difference reward的思想是:保持其他智能体的联合动作不动,把当前智能体的action替换为一个default action,检查值函数Q是否有变化,如果没有,代表当前智能体的action是无贡献的action,因为奖励r不是当前智能体的action获得的。但是difference reward思想有个问题,default action选谁???无法选择!!!为了解决这个问题,COMA定义了优势函数A,解决了多智能体信用分配问题。如果仔细看算法的A函数公式,它其实就是AC算法中常用的优势函数A在多智能体领域的扩展而已。

COMA 与 MADDPG 在 actor network 上的不同之处在于前者使用的是 GRU 网络,为了更好的处理局部观察问题,但是后者使用的则是普通的 DNN。
COMA算法具体框架如下图所示:
网络架构: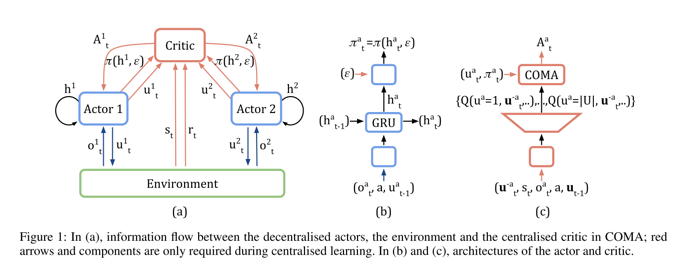
VDN
论文:Value-Decomposition Networks For Cooperative Multi-Agent Learning
VDN(Value-Decomposition Networks)算法是一种用于多智能体强化学习(MARL)的算法。它旨在解决多智能体系统中合作与竞争的问题,其中各个智能体需要同时考虑个体利益与整体目标。
VDN算是大名鼎鼎的QMIX算法的前身。VDN算法假定:Qtot是每个智能体的Qi的算术加和。对于智能体Agenti来说,它只用最大化Qtot函数的子项Qi函数即可。如下图:
左边是IQL,右边是VDN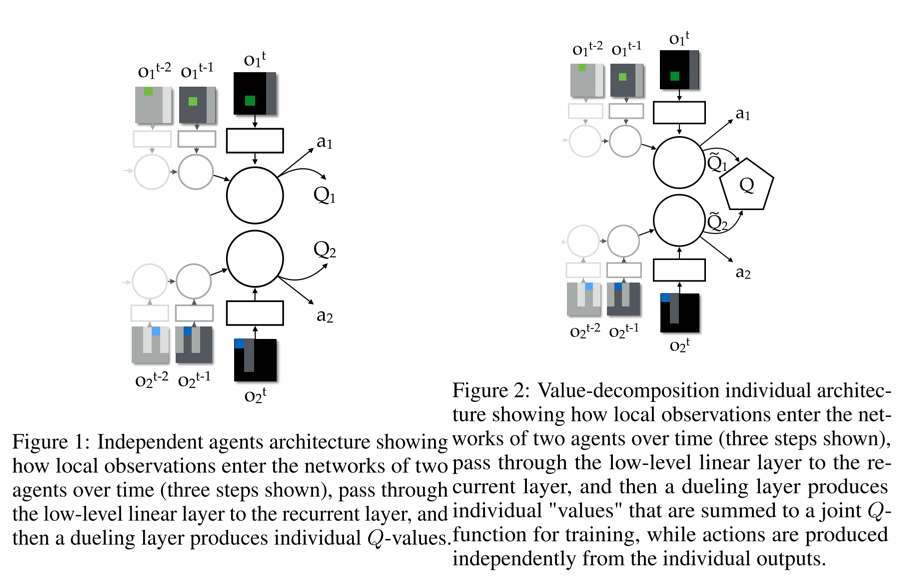
作者假定如下等式成立: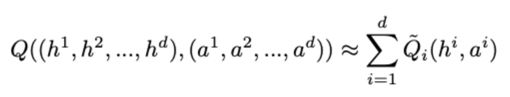
h表示序列观察,a表示序列动作。 注意到,上述分解满足一个很好的性质,即对左边的联合 Q function 进行 操作,等价于对右边每一个局部 Q function 分别进行 。这样可以保证训练完毕后去中心化执行时,即使整个系统只基于局部观察进行决策,其策略也是与基于全局观察进行决策是一致的。
推导上式:
假定整个多智能体系统中包含两个智能体,并且全局回报函数是每个智能体的局部回报函数的加和: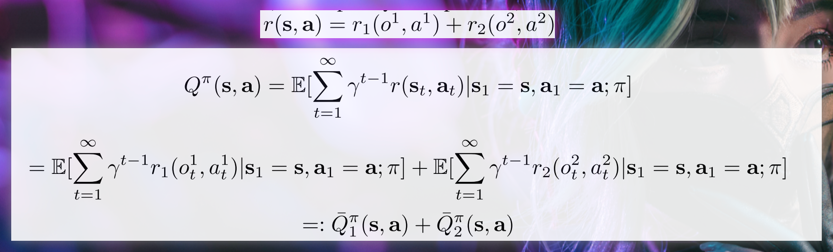
这样分解后的 Q 函数是基于全局观察的。由于使用的网络结构是 LSTM,那么估计误差是可以缩小的,并且还可以通过智能体之间的通信来进一步减小误差,所以本文假设: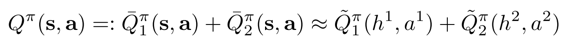
网络架构: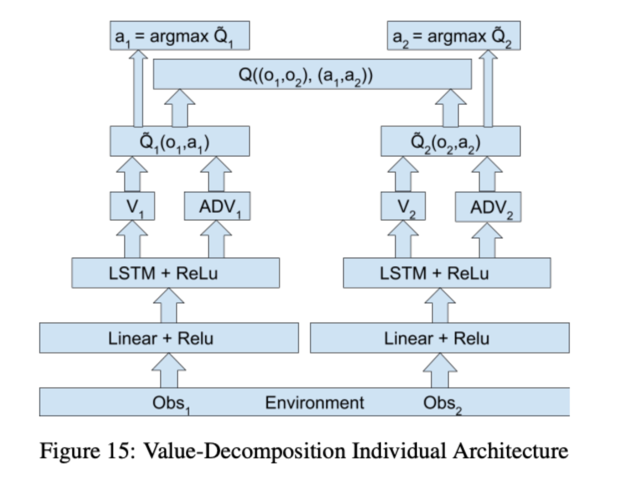
VDN算法强调的是把总的Q相信分解为多个Q之和,每个Q对应每个智能体的动作价值,这种会导致一个结果,那就是这样累计求和的Q可能没有具体的意义、吃大锅饭导致有agent划水之类的结果。这些问题在QMIX中得到了比较好的解决。
QMIX
论文:QMIX: Monotonic Value Function Factorisation for Deep Multi-Agent Reinforcement Learning
深度多智能体强化学习的单调值函数分解
QMIX是一个多智能体强化学习算法,具有如下特点:
- 学习得到分布式策略。
- 本质是一个值函数逼近算法。
- 由于对一个联合动作-状态只有一个总奖励值,而不是每个智能体得到一个自己的奖励值,因此只能用于合作环境,而不能用于竞争对抗环境。
- QMIX算法采用集中式学习,分布式执行应用的框架。通过集中式的信息学习,得到每个智能体的分布式策略。
- 训练时借用全局状态信息来提高算法效果。是后文提到的VDN方法的改进。
- 接上一条,QMIX设计一个神经网络来整合每个智能体的局部值函数而得到联合动作值函数,VDN是直接求和。
- 每个智能体的局部值函数只需要自己的局部观测,因此整个系统在执行时是一个分布式的,通过局部值函数,选出累积期望奖励最大的动作执行。
- 算法使联合动作值函数与每个局部值函数的单调性相同,因此对局部值函数取最大动作也就是使联合动作值函数最大。
- 算法针对的模型是一个分布式多智能体部分可观马尔可夫决策过程(Dec-POMDP)。
背景知识
MARL核心问题
在多智能体强化学习中一个关键的问题就是如何学习联合动作值函数,因为该函数的参数会随着智能体数量的增多而成指数增长,如果动作值函数的输入空间过大,则很难拟合出一个合适函数来表示真实的联合动作值函数。另一个问题就是学得了联合动作值函数后,如何通过联合值函数提取出一个优秀的分布式的策略。这其实是单智能体强化学习拓展到MARL的核心问题。
Dec-POMDP
Dec-POMDP指的是分布式部分可观察马尔可夫决策过程(Decentralized Partially Observable Markov Decision Process)。在 Dec-POMDP 中,有多个智能体同时存在,并且每个智能体只能观察到局部的环境信息,而不能直接获取全局状态。此外,每个智能体的动作会影响整个系统的演变。
IQL
IQL(independent Q-learning)就是非常暴力的给每个智能体执行一个Q-learning算法,因为共享环境,并且环境随着每个智能体策略、状态发生改变,对每个智能体来说,环境是动态不稳定的,因此这个算法也无法收敛,但是在部分应用中也具有较好的效果。
VDN
如前介绍:
DRQN
DRQN是一个用来处理POMDP(部分可观马尔可夫决策过程)的一个算法,其采用LSTM替换DQN卷基层后的一个全连接层,来达到能够记忆历史状态的作用,因此可以在部分可观的情况下提高算法性能。由于QMIX解决的是多智能体的POMDP问题,因此每个智能体采用的是DRQN算法。
QMIX
QMIX是在VDN上的一种拓展,由于VDN只是将每个智能体的局部动作值函数求和相加得到联合动作值函数,虽然满足联合值函数与局部值函数单调性相同的可以进行分布化策略的条件,但是其没有在学习时利用状态信息以及没有采用非线性方式对单智能体局部值函数进行整合,使得VDN算法还有很大的提升空间。QMIX就是采用一个混合网络对单智能体局部值函数进行合并,并在训练学习过程中加入全局状态信息辅助,来提高算法性能。
QMIX约束条件: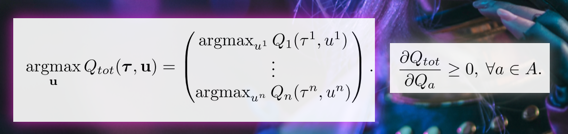
也就是总Q关于每个agent的偏导都必须是正的。也就是,对于每个agent来说,追求自身收益的最大化是没有错误的(都对全局有不小于0的贡献)。
具体网络结构如下: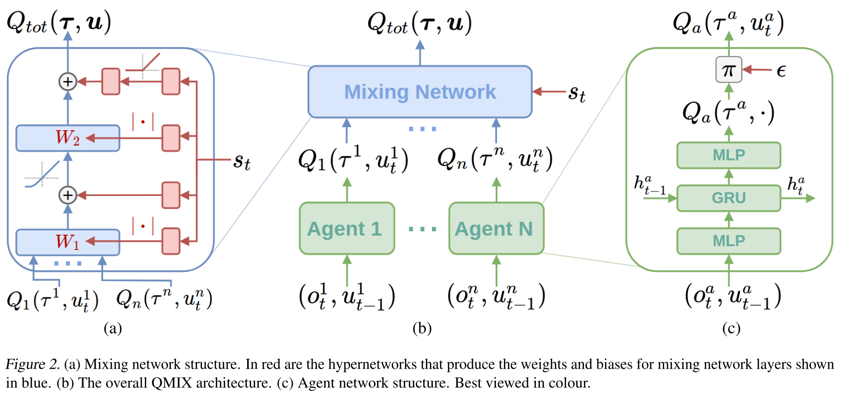
图(c)表示每个智能体采用一个DRQN来拟合自身的Q值函数得到Qi(τi,ai; θi),DRQN循环输入当前的观测oi,t,以及上一时刻的动作ai,t-1来得到Q值。
图(b)表示混合网络的结构。其输入为每个DRQN网络的输出。为了满足上述的单调性约束,混合网络的所有权值都是非负数,对偏移量不做限制,这样就可以确保满足单调性约束。
为了能够更多的利用到系统的状态信息st ,采用一种超网络(hypernetwork),将状态st作为输入,输出为混合网络的权值及偏移量。为了保证权值的非负性,采用一个线性网络以及绝对值激活函数保证输出不为负数。对偏移量采用同样方式但没有非负性的约束,混合网络最后一层的偏移量通过两层网络以及ReLU激活函数得到非线性映射网络。由于状态信息st是通过超网络混合到Qtot中的,而不是仅仅作为混合网络的输入项,这样带来的一个好处是,如果作为输入项则st的系数均为正,这样则无法充分利用状态信息来提高系统性能,相当于舍弃了一半的信息量。
QMIX的Loss: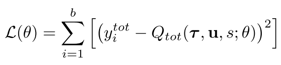
更新用到了传统的DQN的思想,其中b表示从经验记忆中采样的样本数量,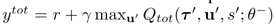
由于满足上文的单调性约束,对Qtot进行argmax 操作的计算量就不在是随智能体数量呈指数增长了,而是随智能体数量线性增长,极大的提高了算法效率。
QTRAN
论文:QTRAN: Learning to Factorize with Transformation for Cooperative Multi-Agent Reinforcement Learning
学习因式分解以实现协作多智能体强化学习 Q-Tran
QMIX 在近似𝑄𝑡𝑜𝑡𝑎𝑙(𝒔, 𝒖)时额外使用了全局状态𝒔,这样就可以基于全局状态𝒔进行训练。但是如果直接将𝒔和[𝑄1, … , 𝑄𝑁]一起输入到神经网络𝑓去得到𝑄𝑡𝑜𝑡𝑎𝑙, 由于前面限制了𝑓中的参数是非负的, 但这会对𝑄𝑡𝑜𝑡𝑎𝑙和𝒔的关系进行不必要的限制,因为只希望局部最优动作就是全局最优动作。QTRAN 聚焦于释放累加性和单调性的限制, 去分解所有可分解的任务。 其思想在于只要保证个体最优动作𝑢̅和联合最优动作𝑢∗是相同的。
QTRAN 认为既然 VDN 和 QMIX 是通过累加或者单调近似得到的𝑄𝑡𝑜𝑡𝑎𝑙, 那么𝑄𝑡𝑜𝑡𝑎𝑙就很有可能与真实的𝑄𝑡𝑜𝑡𝑎𝑙 ∗ 相差很远, 那我不如直接去学习一个真实的𝑄𝑡𝑜𝑡𝑎𝑙 ∗ 。
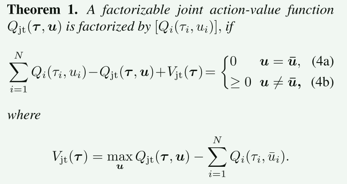
这里的Qjt就是学习得到的,介于各个agent的收益Q之和和实际局面价值之间的联合补偿,建立了局部Q和全局Q之间的联系。
为了满足上述定理,QTRAN 提出了两个算法 QTRAN-base 以及 QTRAN-alt: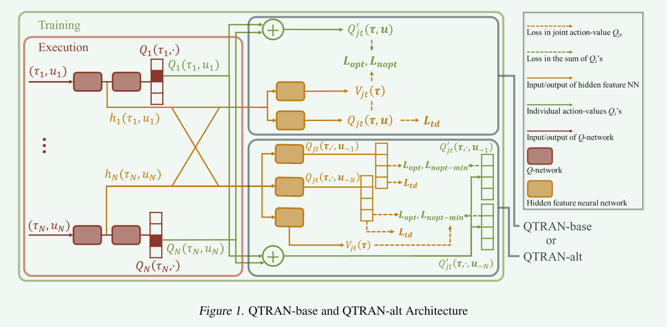
TRAN-base
分为三部分:
- 独立 Q 网络
- 联合 Q 网络
- 联合 V 网络
整体的Loss如下: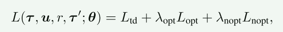
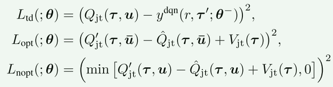
TRAN-alt
QTRAN-alt 是针对 QTRAN(Q-function Transfer)算法的一个改进版本,旨在解决原始 QTRAN 在处理非零约束时的问题。
作者认为约束: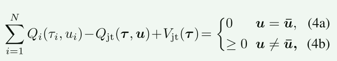
在原始 QTRAN 算法中,对于非零动作的约束(对应公式中的第二个约束),可能会过于松弛,导致算法难以准确地拟合联合 Q 函数。这是因为在训练数据中的数据很少,大部分的数据都可能满足第二个约束。
为了解决这个问题,QTRAN-alt 提出了一个新的定理,将原始约束中的第二个约束替换为一个更强的约束。这个新的约束使得算法能够更准确地拟合联合 Q 函数,从而提升了算法的性能和训练效果。
这个约束更多的聚焦于非0的训练数据(这一部分数据占训练初期训练集的大部分)。为了满足这一约束,需要把上面列出的第三个损失函数替换为:
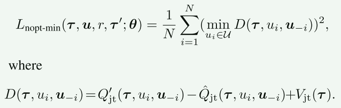
具体来说,QTRAN-alt 对于非零动作的约束更加严格,以提高算法的性能。这种改进使得 QTRAN-alt 在处理合作问题中的分工与协作时表现更为优越。
算法流程:
MFMARL
论文:Mean Field Multi-Agent Reinforcement Learning
平均场多智能体强化学习
MFMARL主要致力于极大规模的多智能体强化学习问题,解决大规模智能体之间的交互及计算困难。由于多智能体强化学习问题不仅有环境交互问题,还有智能体之间的动态影响,因此为了得到最优策略,每个智能体都需要考察其他智能体的动作及状态得到联合动作值函数。由于状态空间跟动作空间随着智能体数量的增多而迅速扩大,这给计算以及探索带来了非常大的困难。
MFMARL算法借用了平均场论(Mean Field Theory,MFT)的思想,其对多智能体系统给出了一个近似假设:对某个智能体,其他所有智能体对其产生的作用可以用一个均值替代。这样就就将一个智能体与其邻居智能体之间的相互作用简化为两个智能体之间的相互作用(该智能体与其所有邻居的均值)。这样极大地简化了智能体数量带来的模型空间的增大。应用平均场论后,学习在两个智能体之间是相互促进的:单个智能体的最优策略的学习是基于智能体群体的动态;同时,集体的动态也根据个体的策略进行更新。
下面具体介绍算法细节,其结合平均场论得出两个主要算法MF-Q与MF-AC,是对Q-learning以及AC算法的改进,并且在理论上给出了收敛性证明,能够收敛到纳什均衡点。该算法可以应用于竞争环境或合作环境,并且每个智能体不知道环境的模型以及奖励模型,但是能够观察邻居智能体的动作及奖励。每个智能体有自己的奖励值。
背景知识
随机博弈

Nash-Q

Mean Field MARL

平均场近似



算法设计
原文中将(7)通过参数化用神经网络进行拟合逼近,与DQN以及AC算法结合,分别给出了MF-Q与MF-AC算法。
MF-Q
通过神经网络拟合(7)式中的Q函数,使用如下所示的代价函数,与DQN中相同,为了减小拟合的Q值与真实Q值之间的误差
对上式求导可以得出参数梯度方向如下: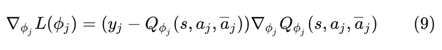
通过梯度下降法可以得到参数更新公式。
算法流程:
MF-AC
类似DPG,使用神经网络拟合一个策略替换玻尔兹曼机通过Q的到的策略,则得到了MF-AC算法。
类似SPG,actor策略梯度公式可以写为: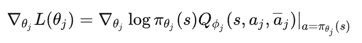
critic类似于MF-Q的更新方式(9)

总结

至此,MARL的入门已结束,后面会结合科研方向看论文想点子。









